Question

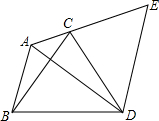已知：如图，在△ABC中，∠BAC=120°，以BC为边向形外作等边△BCD，把△ABD绕着点D按顺时针方向旋转60°后得到△ECD，若AB=3，AC=2．
（1）求证：点A、C、E在一条直线上；
（2）求∠BAD的度数；
（3）求AD的长．

Answer 1

（1）证明：∵△BCD为等边三角形，
∴∠3=∠4=60°，DC=DB，
∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD，
∴∠5=∠1+∠4=∠1+60°，
∴∠2+∠3+∠5=∠2+∠1+120°，
∵∠BAC=120°，
∴∠1+∠2=180°-∠BAC=60°，
∴∠2+∠3+∠5=60°+120°=180°，
∴点A、C、E在一条直线上；

（2）解：∵点A、C、E在一条直线上，
而△ABD绕着点D按顺时针方向旋转60°后得到△ECD，
∴∠ADE=60°，DA=DE，
∴△ADE为等边三角形，
∴∠DAE=60°，
∴∠BAD=∠BAC-∠DAE=120°-60°=60°，；

（3）解：∵点A、C、E在一条直线上，
∴AE=AC+CE，
∵△ABD绕着点D按顺时针方向旋转60°后得到△ECD，
∴CE=AB，
∴AE=AC+AB=2+3=5，
∵△ADE为等边三角形，
∴AD=AE=5．
分析：（1）根据等边三角形的性质由△BCD为等边三角形得到∠3=∠4=60°，DC=DB，再根据旋转的性质得到∠5=∠1+∠4=∠1+60°，则∠2+∠3+∠5=∠2+∠1+120°，再根据三角形内角和定理得到
∠1+∠2=180°-∠BAC=60°，于是∠2+∠3+∠5=60°+120°=180°，即可得到点A、C、E在一条直线上；
（2）由于点A、C、E在一条直线上，△ABD绕着点D按顺时针方向旋转60°后得到△ECD，则∠ADE=60°，DA=DE，得到△ADE为等边三角形，则∠DAE=60°，然后利用∠BAD=∠BAC-∠DAE计算即可；
（3）由于点A、C、E在一条直线上，则AE=AC+CE，根据旋转的性质得到CE=AB，则AE=AC+AB=2+3=5，而△ADE为等边三角形，则AD=AE=5．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等边三角形的判定与性质．