题目内容
一种产品，原来每件售价是81元，由于求过供，所以产品连续两次涨价，现售价是100元，则平均每次的增长率为________%（精确到0.1）
11.1
分析：如果设平均每次的增长率是x，那么这种产品第一次涨价后的价格为81（1+x）元，第二次涨价后的价格为81（1+x）2元，而此时的价格为100元，根据这个等量关系可以列出方程．
解答：设平均每次的增长率为x．
依题意，得81（1+x）2=100，
解方程，得x1=
≈11.1%，x2=-
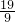（舍去）．
故平均每次的增长率约为11.1%．
点评：本题考查数量平均变化率问题．原来的数量（价格）为a，平均每次增长或降低的百分率为x的话，经过第一次调整，就调整到a（1±x），再经过第二次调整就是a（1±x）（1±x）=a（1±x）2．增长用“+”，下降用“-”．
分析：如果设平均每次的增长率是x，那么这种产品第一次涨价后的价格为81（1+x）元，第二次涨价后的价格为81（1+x）2元，而此时的价格为100元，根据这个等量关系可以列出方程．
解答：设平均每次的增长率为x．
依题意，得81（1+x）2=100，
解方程，得x1=
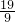≈11.1%，x2=-（舍去）．故平均每次的增长率约为11.1%．
点评：本题考查数量平均变化率问题．原来的数量（价格）为a，平均每次增长或降低的百分率为x的话，经过第一次调整，就调整到a（1±x），再经过第二次调整就是a（1±x）（1±x）=a（1±x）2．增长用“+”，下降用“-”．
练习册系列答案
全能练考卷系列答案
相关题目
某公司生产的A种产品，每件成本是2元，每件售价是3元，一年的销售量是10万件．为了获得更多的利润，公司准备拿出一定资金来做广告．根据经验，每年投入的广告费为x（万元）时，产品的年销售量是原来的y倍，且y是x的二次函数，公司作了预测，知x与y之间的对应关系如下表：
（1）根据上表，求y关于x的函数关系式；
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润S（万元）与广告费x（万元）的函数关系式；
（3）从上面的函数关系式中，你能得出什么结论？
| x（万元） | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润S（万元）与广告费x（万元）的函数关系式；
（3）从上面的函数关系式中，你能得出什么结论？