题目内容
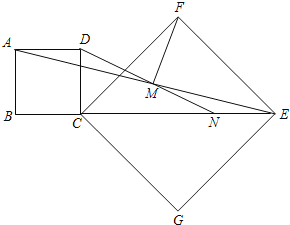
【题目】如图,正方形CGEF的对角线CE在正方形ABCD的边BC的延长线上(CG>BC),M是线段AE的中点,DM的延长线交CE于N.
(1)求证:AD=NE
(2)求证:①DM=MF;②DM⊥MF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题
(1)由已知条件证:△ADM≌△ENM可得AD=NE;
(2)连接FD、FN,结合(1)中所得结论和已知条件可证△CDF≌△ENF,从而可得:FD=FN,∠3=∠4,由此可得:∠3+∠CFN=∠4+∠CFN=∠CFE=90°,这样可证得:△DFN是等腰直角三角形;再由△ADM≌△ENM可得DM=NM,就可得到:FM是等腰直角△DFN斜边上的中线,就可得到;DM=MF,DM⊥MF.
试题解析:
(1)∵四边形ABCD是正方形,
∴AD∥BC,∠BCD=90°,AD=CD,
∴∠MAD=∠MEN,
又∵M是AE的中点,
∴AM=EM
在△ADM和△ENM中,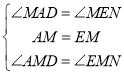 ,
,
∴△ADM≌△ENM(ASA),
∴AD=EN;
(2)连接FD、FN,
∵CE是正方形CGEF的对角线,
∴CF=EF,∠1=∠FEN=45°,
又∵∠BCD=90°,
∴∠DCE=90°,
∴∠2=∠1=∠FEN=45°,
在△CDF和△ENF中,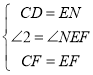 ,
,
∴△CDF≌△ENF(SAS)
∴∠3=∠4,DF=FN,
又∵∠CFN+∠4=90°,
∴∠CFN+∠3=90°,
∴△DFN是等腰直角三角形,
∵△ADM≌△ENM,
∴DM=NM,
∴FM=DM,FM⊥DM.

 字词句段篇系列答案
字词句段篇系列答案【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?