题目内容
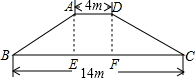
如图梯形ABCD的两底长为AD=6,BC=10,中线为EF,且∠B=90°,若P为AB上的一点,且PE将梯形ABCD分成面积相同的两区域,则△EFP与梯形ABCD的面积比为( )

| A.1:6 | B.1:10 | C.1:12 | D.1:16 |

∵梯形ABCD的两底长为AD=6,BC=10,
∴EF=
(AD+BC)=
×(6+10)=8,
∴S梯形ABCD=
(AD+BC)×AB=
×(6+10)×AB=8AB.
S梯形AFED=
(AD+EF)×
AB=
(6+8)×AB=
AB,
∴S△EFP=
S梯形ABCD-S梯形AFED=4AB-
AB=
AB,
∴S△EFP:S梯形ABCD=
:8=1:16.
故选D.
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
S梯形AFED=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 7 |
| 2 |
∴S△EFP=
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
∴S△EFP:S梯形ABCD=
| 1 |
| 2 |
故选D.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目