题目内容
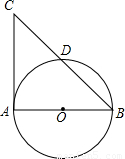
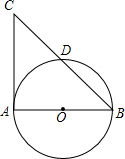已知如图，AB、AC分别是⊙O的直径和切线，BC交⊙O于D．AB=8，AC=6，则CD的长为（ ）| A、3 | B、4 | C、9 | D、3.6 |
分析：先连接AD，由于AB是直径，AC是切线，那么可知∠ADB=90°，∠CAB=90°，在Rt△ABC中利用勾股定理易求BC，而∠ABD=∠CBA，∠ADB=∠CAB，易证△ABD∽△CBA，利用比例线段可求BD，进而可求CD．
解答：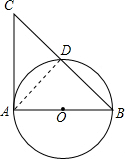
解：如右图所示，连接AD，
∵AB是直径，AC是切线，
∴∠ADB=90°，∠CAB=90°，
在Rt△ABC中，AC=6，AB=8，那么BC=
=10，
∵∠ABD=∠CBA，∠ADB=∠CAB，
∴△ABD∽△CBA，
∴AB：BD=BC：AB，
∴BD=
=
=
，
∴CD=BC-BD=10-
=
=3.6．
故选D．
解：如右图所示，连接AD，∵AB是直径，AC是切线，
∴∠ADB=90°，∠CAB=90°，
在Rt△ABC中，AC=6，AB=8，那么BC=
| AC2+AB2 |
∵∠ABD=∠CBA，∠ADB=∠CAB，
∴△ABD∽△CBA，
∴AB：BD=BC：AB，
∴BD=
| AB2 |
| BC |
| 64 |
| 10 |
| 32 |
| 5 |
∴CD=BC-BD=10-
| 32 |
| 5 |
| 18 |
| 5 |
故选D．
点评：本题考查了勾股定理、圆周角定理、切线的性质、相似三角形的判定和性质．解题的关键是连接AD，构造直角三角形．
练习册系列答案
相关题目
