题目内容
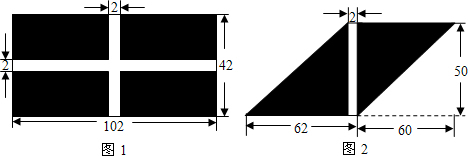
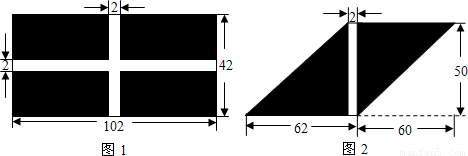
为了参加市教委举行的“争创绿色学校,美化校园环境”的活动,某区教委决定委托园林公司对所辖甲、乙两所学校进行校园绿化工作.已知甲校有如图1所示的矩形内阴影部分空地需铺设草坪,乙校有如图2所示的平行四边形内阴影部分空地需铺设草坪(图1,图2中数据单位均为“米”).在A、B两地分别有同种草皮4500米2和2500米2出售,且售价一样.若园林公司向A、B两地购买草皮,其路程和运费单价表如下:
| 甲校 | 乙校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| A地 | 20 | 0.3 | 10 | 0.3 |
| B地 | 15 | 0.2 | 20 | 0.2 |
(1)分别求出图1、图2的阴影部分面积;
(2)若甲校从A地购买x米2的草皮(x取整数),因路程关系,甲校从A地购买的草皮数不超过甲校从B地购买的草皮数,乙校从B地购买的草皮数大于甲校从B地购买的草皮数的
 ,那么甲校乙校从A,B两地购买草皮的方案有多少种?
,那么甲校乙校从A,B两地购买草皮的方案有多少种?(3)在(2)的条件下,请你设计出总运费最低的草皮运送方案,并说明理由.

解:(1)图1的阴影部分面积为102×42-(102+42)×2+2×2=4000米2,
图2的阴影部分面积为62×50-2×50=3000米2;
(2)由题意列不等式组,
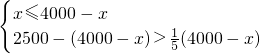 ,
,
解得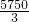 <x≤2000,
<x≤2000,
因为x取整数,所以x的值为1917、1918、1919、…、2000共84种方案;
(3)若甲校从A地购买x米2,
则总运费为0.3×20x+0.3×10(4500-x)+0.2×15(4000-x)+0.2×20(x-1500)=4x+19500,
由(2)可知x的最小值为1917,
所以当x=1917时,总运费最低为4×1917+19500=27168元.
分析:(1)利用矩形的面积与平行四边形的面积解答即可;
(2)根据题意列出不等式组解答即可;
(3)分别从用量,路程的远近,每平方米的运费分析比较即可解决问题.
点评:此题主要考查一元一次不等式组的运用,矩形和平行四边形的面积以及方案选择等问题.
图2的阴影部分面积为62×50-2×50=3000米2;
(2)由题意列不等式组,
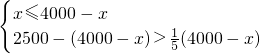 ,
,解得
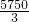 <x≤2000,
<x≤2000,因为x取整数,所以x的值为1917、1918、1919、…、2000共84种方案;
(3)若甲校从A地购买x米2,
则总运费为0.3×20x+0.3×10(4500-x)+0.2×15(4000-x)+0.2×20(x-1500)=4x+19500,
由(2)可知x的最小值为1917,
所以当x=1917时,总运费最低为4×1917+19500=27168元.
分析:(1)利用矩形的面积与平行四边形的面积解答即可;
(2)根据题意列出不等式组解答即可;
(3)分别从用量,路程的远近,每平方米的运费分析比较即可解决问题.
点评:此题主要考查一元一次不等式组的运用,矩形和平行四边形的面积以及方案选择等问题.

练习册系列答案
相关题目
为了参加市教委举行的“争创绿色学校,美化校园环境”的活动,某区教委决定委托园林公司对所辖甲、乙两所学校进行校园绿化工作.已知甲校有如图1所示的矩形内阴影部分空地需铺设草坪,乙校有如图2所示的平行四边形内阴影部分空地需铺设草坪(图1,图2中数据单位均为“米”).在A、B两地分别有同种草皮4500米2和2500米2出售,且售价一样.若园林公司向A、B两地购买草皮,其路程和运费单价表如下:
(注:运费单价表示每平方米草皮运送1千米所需要的人民币)
(1)分别求出图1、图2的阴影部分面积;
(2)若甲校从A地购买x米2的草皮(x取整数),因路程关系,甲校从A地购买的草皮数不超过甲校从B地购买的草皮数,乙校从B地购买的草皮数大于甲校从B地购买的草皮数的
,那么甲校乙校从A,B两地购买草皮的方案有多少种?
(3)在(2)的条件下,请你设计出总运费最低的草皮运送方案,并说明理由.
| 甲校 | 乙校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| A地 | 20 | 0.3 | 10 | 0.3 |
| B地 | 15 | 0.2 | 20 | 0.2 |
(1)分别求出图1、图2的阴影部分面积;
(2)若甲校从A地购买x米2的草皮(x取整数),因路程关系,甲校从A地购买的草皮数不超过甲校从B地购买的草皮数,乙校从B地购买的草皮数大于甲校从B地购买的草皮数的
| 1 |
| 5 |
(3)在(2)的条件下,请你设计出总运费最低的草皮运送方案,并说明理由.

为了参加市教委举行的“争创绿色学校,美化校园环境”的活动,某区教委决定委托园林公司对所辖甲、乙两所学校进行校园绿化工作.已知甲校有如图1所示的矩形内阴影部分空地需铺设草坪,乙校有如图2所示的平行四边形内阴影部分空地需铺设草坪(图1,图2中数据单位均为“米”).在A、B两地分别有同种草皮4500米2和2500米2出售,且售价一样.若园林公司向A、B两地购买草皮,其路程和运费单价表如下:
(注:运费单价表示每平方米草皮运送1千米所需要的人民币)
(1)分别求出图1、图2的阴影部分面积;
(2)若甲校从A地购买x米2的草皮(x取整数),因路程关系,甲校从A地购买的草皮数不超过甲校从B地购买的草皮数,乙校从B地购买的草皮数大于甲校从B地购买的草皮数的 ,那么甲校乙校从A,B两地购买草皮的方案有多少种?
,那么甲校乙校从A,B两地购买草皮的方案有多少种?
(3)在(2)的条件下,请你设计出总运费最低的草皮运送方案,并说明理由.
| 甲校 | 乙校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| A地 | 20 | 0.3 | 10 | 0.3 |
| B地 | 15 | 0.2 | 20 | 0.2 |
(1)分别求出图1、图2的阴影部分面积;
(2)若甲校从A地购买x米2的草皮(x取整数),因路程关系,甲校从A地购买的草皮数不超过甲校从B地购买的草皮数,乙校从B地购买的草皮数大于甲校从B地购买的草皮数的
 ,那么甲校乙校从A,B两地购买草皮的方案有多少种?
,那么甲校乙校从A,B两地购买草皮的方案有多少种?(3)在(2)的条件下,请你设计出总运费最低的草皮运送方案,并说明理由.
