题目内容
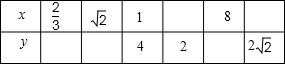
下表给出了x与函数y=x2+bx+c的一些对应值:| x | … | 0 | 1 | 3 | 6 | … |
| y | … | 5 | 0 | -4 | 5 | … |
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.
分析:(1)利用待定系数法,把三组对应值代入,解方程组即可求解;
(2)表中的(0,5)和(6,5)关于对称轴对称,即可求得对称轴,然后把对称轴对应的数值代入函数解析式,即可求得顶点的纵坐标;
(3)在解析式中令y=0,即可求得横坐标,纵坐标是0;
(4)根据图象写出位于x轴下方的部分x的范围.
(2)表中的(0,5)和(6,5)关于对称轴对称,即可求得对称轴,然后把对称轴对应的数值代入函数解析式,即可求得顶点的纵坐标;
(3)在解析式中令y=0,即可求得横坐标,纵坐标是0;
(4)根据图象写出位于x轴下方的部分x的范围.
解答: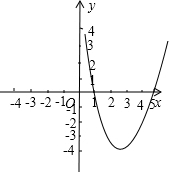 解:(1)根据题意得:
解:(1)根据题意得:
解得:
则函数的解析式是:y=x2-6x+5;
(2)对称轴是:x=
=3,
把x=3代入函数解析式得:y=9-18+5=-4,
则函数的顶点是(3,-4);
(3)在y=x2-6x+5中,
令y=0,解得:x=1或5.
则与x轴的交点坐标是:(1,0)和(5,0);
(4)根据图象可得:当y<0时,x的范围是:1<x<5.
 解:(1)根据题意得:
解:(1)根据题意得:
|
解得:
|
则函数的解析式是:y=x2-6x+5;
(2)对称轴是:x=
| 0+6 |
| 2 |
把x=3代入函数解析式得:y=9-18+5=-4,
则函数的顶点是(3,-4);
(3)在y=x2-6x+5中,
令y=0,解得:x=1或5.
则与x轴的交点坐标是:(1,0)和(5,0);
(4)根据图象可得:当y<0时,x的范围是:1<x<5.
点评:本题主要考查了待定系数法求二次函数的解析式,以及对称轴,顶点坐标的求法,结合图象确定自变量的取值范围,是一个基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
下表给出了x与函数y=x2+bx+c的一些对应值:
| x | … | 0 | 1 | 3 | 6 | … |
| y | … | 5 | 0 | -4 | 5 | … |
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.
下表给出了x与函数y=x2+bx+c的一些对应值:
(1)请根据表格求出y=x2+bx+c的解析式;
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.
| x | … | 1 | 3 | 6 | … | |
| y | … | 5 | -4 | 5 | … |
(2)写出抛物线y=x2+bx+c的对称轴与顶点坐标;
(3)求出y=x2+bx+c与x轴的交点坐标;
(4)画出y=x2+bx+c的大致图象,并结合图象指出,当y<0,x的取值范围.