题目内容
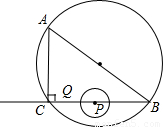
如图,已知⊙O为△ABC的外接圆,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.(1)试说明圆心O的位置.
(2)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
(3)若⊙P与⊙O相切,求t的值.
【答案】分析:(1)根据直角三角形的性质以及圆周角定理得出圆心O的位置为线段AB的中点;
(2)首先根据勾股定理得出AB的长,再利用△PBD∽△ABC,得出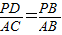 ,求出PD的长;即圆心P到直线AB的距离等于⊙P的半径,得出答案即可;
,求出PD的长;即圆心P到直线AB的距离等于⊙P的半径,得出答案即可;
(3)根据点P在⊙O内部,得出⊙P与⊙O只能内切,进而利用半径与圆心距之间的关系求出即可.
解答: 解:(1)如图1,∵Rt△ABC中,∠ACB=90°,AB是△ABC外接圆直径,
解:(1)如图1,∵Rt△ABC中,∠ACB=90°,AB是△ABC外接圆直径,
∴圆心O的位置为线段AB的中点.
(2)直线AB与⊙P相切.
如图2,过点P作PD⊥AB,垂足为D.
在Rt△ABC中,∠ACB=90°
∵AC=6cm,BC=8cm
∴AB= =10(cm),
=10(cm),
∵P为BC的中点
∴PB=4cm.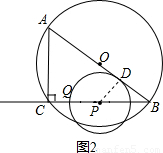
∵∠PDB=∠ACB=90°,∠PBD=∠ABC
∴△PBD∽△ABC.
∴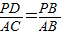 ,即
,即
∴PD=2.4(cm).
当t=1.2时,PQ=2t=2.4(cm)
∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径.
∴直线AB与⊙P相切.
(3)∵∠ACB=90°,
∴AB为△ABC的外切圆的直径.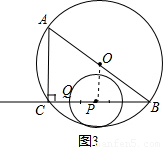
∴OB= AB=5(cm).
AB=5(cm).
如图3,连接OP,
∵P为BC的中点,O为BA的中点,
∴OP= AC=3(cm).
AC=3(cm).
∵点P在⊙O内部,
∴⊙P与⊙O只能内切.
∴5-2t=3或2t-5=3,
∴t=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
点评:此题主要考查了相切两圆的性质以及切线的判定和圆周角定理等知识,利用图形分类讨论得出是解题关键.
(2)首先根据勾股定理得出AB的长,再利用△PBD∽△ABC,得出
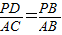 ,求出PD的长;即圆心P到直线AB的距离等于⊙P的半径,得出答案即可;
,求出PD的长;即圆心P到直线AB的距离等于⊙P的半径,得出答案即可;(3)根据点P在⊙O内部,得出⊙P与⊙O只能内切,进而利用半径与圆心距之间的关系求出即可.
解答:
 解:(1)如图1,∵Rt△ABC中,∠ACB=90°,AB是△ABC外接圆直径,
解:(1)如图1,∵Rt△ABC中,∠ACB=90°,AB是△ABC外接圆直径,∴圆心O的位置为线段AB的中点.
(2)直线AB与⊙P相切.
如图2,过点P作PD⊥AB,垂足为D.
在Rt△ABC中,∠ACB=90°
∵AC=6cm,BC=8cm
∴AB=
 =10(cm),
=10(cm),∵P为BC的中点
∴PB=4cm.

∵∠PDB=∠ACB=90°,∠PBD=∠ABC
∴△PBD∽△ABC.
∴
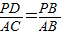 ,即
,即
∴PD=2.4(cm).
当t=1.2时,PQ=2t=2.4(cm)
∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径.
∴直线AB与⊙P相切.
(3)∵∠ACB=90°,
∴AB为△ABC的外切圆的直径.

∴OB=
 AB=5(cm).
AB=5(cm).如图3,连接OP,
∵P为BC的中点,O为BA的中点,
∴OP=
 AC=3(cm).
AC=3(cm).∵点P在⊙O内部,
∴⊙P与⊙O只能内切.
∴5-2t=3或2t-5=3,
∴t=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
点评:此题主要考查了相切两圆的性质以及切线的判定和圆周角定理等知识,利用图形分类讨论得出是解题关键.

练习册系列答案
相关题目
 如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是
如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是 如图,已知AB为⊙O的弦,以OB为直径作⊙O1交AB于D,⊙O的弦AE切⊙O1于点C.
如图,已知AB为⊙O的弦,以OB为直径作⊙O1交AB于D,⊙O的弦AE切⊙O1于点C. 如图,已知AB为⊙O的直径,直线BC与⊙O相切于点B,过A作AD∥OC交⊙O于点D,连接CD.
如图,已知AB为⊙O的直径,直线BC与⊙O相切于点B,过A作AD∥OC交⊙O于点D,连接CD. 如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的. 如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.