题目内容
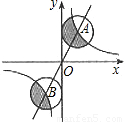
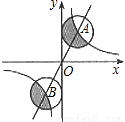
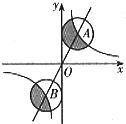
图中正比例函数和反比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆．若点A的坐标为（1，2），则图中两个阴影面积的和是 ．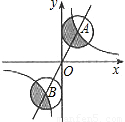
【答案】分析：根据反比例函数的图象关于坐标原点对称，是中心对称图形可得：图中两个阴影面积的和是圆的面积．
解答：解：若点A的坐标为（1，2），即圆的半径为1；
由反比例函数的对称性可得：两个阴影面积的和是S=π×12=π．
故答案为：π．
点评：解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系．
解答：解：若点A的坐标为（1，2），即圆的半径为1；
由反比例函数的对称性可得：两个阴影面积的和是S=π×12=π．
故答案为：π．
点评：解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系．
练习册系列答案
名校课堂系列答案
相关题目
16、图中正比例函数和反比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆．若点A的坐标为（1，2），则图中两个阴影面积的和是
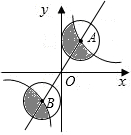图中正比例函数和反比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆，若点A的坐标为（1，2），则图中两个阴影部分面积的和是（ ）A、
| ||
| B、π | ||
| C、4π | ||
| D、条件不足，无法求 |
