题目内容
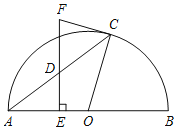
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
【答案】D
【解析】
先利用含30度的直角三角形三边的关系得AC=2![]() ,再利用基本作图得到FG垂直平分AC,CH=CF,则FA=FC,所以∠A=∠FCA=30°,接着证明△BCF为等边三角形,所以CF=CB=2,然后计算AC﹣CH即可.
,再利用基本作图得到FG垂直平分AC,CH=CF,则FA=FC,所以∠A=∠FCA=30°,接着证明△BCF为等边三角形,所以CF=CB=2,然后计算AC﹣CH即可.
在Rt△ABC中,∵∠A=30°,
∴∠B=60°,AC=![]() BC=2
BC=2![]() ,
,
由作法得FG垂直平分AC,CH=CF,
∴FA=FC,
∴∠A=∠FCA=30°,
∴∠BCF=60°,
∴△BCF为等边三角形,
∴CF=CB=2,
∴AH=AC﹣CH=2![]() ﹣2.
﹣2.
故选:D.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】启明公司生产某种产品,每件成本是3元,售价是4元,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x( 万元)时,产品的年销售量是原销售量的y倍,且y=![]() . 如果把利润看作是销售总额减去成本和广告费:
. 如果把利润看作是销售总额减去成本和广告费:
(1)试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广告费是多少万元时,公司获得的年利润最大?最大年利润是多少万元?
(2)把(1)中的最大利润留出3万元做广告,其余的资金投资新项目,现有6个项目可供选择,各项目每股投资金额和预计年收益如下表:
项目 | A | B | C | D | E | F |
每股(万元) | 5 | 2 | 6 | 4 | 6 | 8 |
收益(万元) | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 1 |
如果每个项目只能投一股,且要求所有投资项目的收益总额不得低于1.6万元, 问有几种符合要求的方式?写出每种投资方式所选的项目.