题目内容
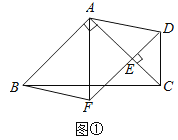
【题目】如图1,抛物线y1=![]() x2+bx+c经过原点,交x轴于另一点A(4,0),顶点为P.
x2+bx+c经过原点,交x轴于另一点A(4,0),顶点为P.
(1)求抛物线y1的解析式和点P的坐标;
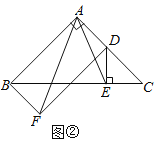
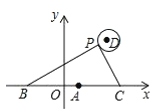
(2)如图2,点Q(0,a)为y轴正半轴上一点,过点Q作x轴的平行线交抛物线y1=![]() x2+bx+c于点M,N,将抛物线y1=
x2+bx+c于点M,N,将抛物线y1=![]() x2+bx+c沿直线MN翻折得到新的抛物线y2,点P落在点B处,若四边形BMPN的面积等于
x2+bx+c沿直线MN翻折得到新的抛物线y2,点P落在点B处,若四边形BMPN的面积等于![]() ,求a的值及点B的坐标;
,求a的值及点B的坐标;
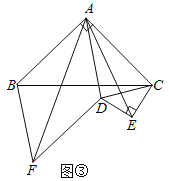
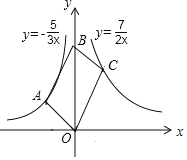
(3)如图3,在(2)的条件下,在第一象限的抛物线y1=![]() x2+bx+c上取一点C,连接OC,作CD⊥OB于D,BE⊥OC交x轴于E,连接DE,若∠BEO=∠DEA,求点C的坐标.
x2+bx+c上取一点C,连接OC,作CD⊥OB于D,BE⊥OC交x轴于E,连接DE,若∠BEO=∠DEA,求点C的坐标.

【答案】(1)y1=![]() x
x![]() -
-![]() x,点P的坐标(2,﹣
x,点P的坐标(2,﹣![]() );(2)B(2,2);(3)C(5,1)
);(2)B(2,2);(3)C(5,1)
【解析】
(1)根据抛物线y1=![]() x2+bx+c经过原点和交x轴于另一点A(4,0),即可求出抛物线y1的解析为
x2+bx+c经过原点和交x轴于另一点A(4,0),即可求出抛物线y1的解析为![]() ,点P的坐标
,点P的坐标![]() ;
;
(2)四边形BMPN的面积等于![]() ,所以
,所以![]() ,联立
,联立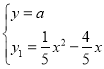 ,化简得 x2-4x-5a=0,MN=|x1-x2|=
,化简得 x2-4x-5a=0,MN=|x1-x2|=![]() ,S△MNP
,S△MNP![]() ,解得a=
,解得a=![]() ,所以B(2,2);
,所以B(2,2);
(3)延长DC与x轴交于点F,∵B(2,2),直线OB:y=x,设点C的坐标![]() ,则直线CD:
,则直线CD:![]() ,直线OC:
,直线OC:![]() ,所以点F
,所以点F![]() ,
,![]() ,易证△BOE~△DFE,则
,易证△BOE~△DFE,则![]() ,求得m=5或m=4(舍去),所以C(5,1).
,求得m=5或m=4(舍去),所以C(5,1).
解:(1)∵抛物线y1=![]() x2+bx+c经过原点,交x轴于另一点A(4,0),
x2+bx+c经过原点,交x轴于另一点A(4,0),
∴
解得![]() ,
,
则抛物线y1的解析为![]() ,点P的坐标
,点P的坐标![]() ;
;
(2)四边形BMPN的面积等于![]() ,所以
,所以![]() ,联立
,联立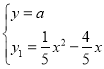
化简得x2-4x-5a=0,MN=|x1-x2|=![]() ,
,
S△MNP![]() ,
,
解得a=![]() ,所以B(2,2);
,所以B(2,2);
(3)延长DC与x轴交于点F,
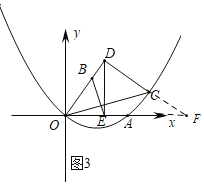
∵B(2,2),
∴直线OB:y=x,
设点C的坐标![]() ,
,
∵CD⊥OB,
∴直线CD:![]() ,
,
直线OC:![]() ,
,
∴点F![]() ,
,
![]() ,
,
∵BE⊥OC,
∴直线BE:![]() ,
,
∴点![]() ,
,
![]() ,
,
∵∠BEO=∠DEA,∠BOE=∠DFE=45°,
∴△BOE~△DFE,
![]() ,
,
即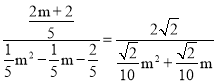 ,
,
解得m=5或m=4(舍去),
所以C(5,1).

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案