题目内容
(2007•徐州)如图,△ABC中,点D在AC上,点E在BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转得到△CD′E′(使∠BCE′<180°),连接AD′、BE′,设直线BE′与AC、AD′分别交于点O、E.(1)若△ABC为等边三角形,则
 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数;(2)若△ABC满足∠ACB=60°,AC=
 ,BC=
,BC=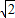 ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
【答案】分析:(1)求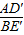 的值,可以通过证明△CBE′≌△CAD′,得到AD′=BE′求出,求∠AFB的度数,通过△AOF与△BOC比较得出;
的值,可以通过证明△CBE′≌△CAD′,得到AD′=BE′求出,求∠AFB的度数,通过△AOF与△BOC比较得出;
(2)求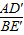 的值和∠AFB的度数,可以通过证明△CBE′∽△CAD′得到;要求△OBC面积的最大值,因为∠ACB=60°,BC=
的值和∠AFB的度数,可以通过证明△CBE′∽△CAD′得到;要求△OBC面积的最大值,因为∠ACB=60°,BC=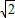 ,即求CO的最大值,用面积公式结合三角函数可以得出.
,即求CO的最大值,用面积公式结合三角函数可以得出.
解答:解:(1)连接D'E',
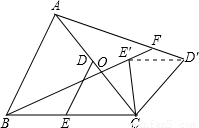
∵△ABC为等边三角形,DE∥AB,
∴△CED,△CD'E'为等边三角形.
∴CD'=CE',∠BCA+∠ACE′=∠D′CE′+∠ACE′即∠BCE′=∠D′CA,AC=CB
∴△CBE′≌△CAD′(SAS),
∴∠CAF=∠CBO,AD′=BE′,
∴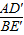 的值为1,
的值为1,
∵∠CAF=∠CBO,
∴∠ABO+∠BAF=120°,
∴∠AFB=60°.
(2)∵AC= ,BC=
,BC=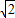 ,DE∥AB,
,DE∥AB,
∴CA:CB=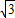 :
: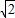 ,CD:CE=
,CD:CE=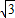 :
: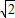 =CD′:CE′,
=CD′:CE′,
∴CA:CB=CD′:CE′=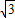 :
: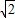 ,
,
∵∠BCE′=∠D′CA,
∴△CBE′∽△CAD′,
∴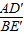 =
=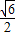 ,∠CBF=∠CAD′,
,∠CBF=∠CAD′,
∵∠BOC=∠AOF,
∴∠AFB=∠ACB=60°:当CO=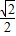 ,△OBC面积的最大值=0.5BC•sin∠ACB•CO=
,△OBC面积的最大值=0.5BC•sin∠ACB•CO=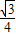 .
.
点评:本题考查了图形的旋转变化,旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.同时综合考查了等边三角形的性质,全等三角形,相似三角形的性质.
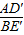 的值,可以通过证明△CBE′≌△CAD′,得到AD′=BE′求出,求∠AFB的度数,通过△AOF与△BOC比较得出;
的值,可以通过证明△CBE′≌△CAD′,得到AD′=BE′求出,求∠AFB的度数,通过△AOF与△BOC比较得出;(2)求
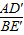 的值和∠AFB的度数,可以通过证明△CBE′∽△CAD′得到;要求△OBC面积的最大值,因为∠ACB=60°,BC=
的值和∠AFB的度数,可以通过证明△CBE′∽△CAD′得到;要求△OBC面积的最大值,因为∠ACB=60°,BC=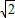 ,即求CO的最大值,用面积公式结合三角函数可以得出.
,即求CO的最大值,用面积公式结合三角函数可以得出.解答:解:(1)连接D'E',

∵△ABC为等边三角形,DE∥AB,
∴△CED,△CD'E'为等边三角形.
∴CD'=CE',∠BCA+∠ACE′=∠D′CE′+∠ACE′即∠BCE′=∠D′CA,AC=CB
∴△CBE′≌△CAD′(SAS),
∴∠CAF=∠CBO,AD′=BE′,
∴
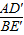 的值为1,
的值为1,∵∠CAF=∠CBO,
∴∠ABO+∠BAF=120°,
∴∠AFB=60°.
(2)∵AC=
 ,BC=
,BC=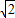 ,DE∥AB,
,DE∥AB,∴CA:CB=
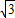 :
: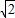 ,CD:CE=
,CD:CE=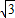 :
: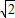 =CD′:CE′,
=CD′:CE′,∴CA:CB=CD′:CE′=
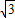 :
: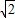 ,
,∵∠BCE′=∠D′CA,
∴△CBE′∽△CAD′,
∴
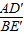 =
=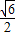 ,∠CBF=∠CAD′,
,∠CBF=∠CAD′,∵∠BOC=∠AOF,
∴∠AFB=∠ACB=60°:当CO=
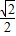 ,△OBC面积的最大值=0.5BC•sin∠ACB•CO=
,△OBC面积的最大值=0.5BC•sin∠ACB•CO=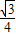 .
.点评:本题考查了图形的旋转变化,旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.同时综合考查了等边三角形的性质,全等三角形,相似三角形的性质.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
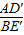 的值为1,求∠AFB的度数;
的值为1,求∠AFB的度数; ,BC=
,BC= ,①求
,①求 的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.
的值和∠AFB的度数;②若E为BC的中点,求△OBC面积的最大值.

 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
