题目内容
甲、乙两人从相距36千米的A、B两地同时出发,相向而行.甲从A地出发1千米后,发现有一物品丢在A地,便立即返回取了物品向B地行进,结果恰好在A、B两地的中点处与乙相遇.已知甲比乙每小时多行0.5千米,设乙的速度为x千米/时,则由题意可列方程为
- A.

- B.
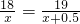
- C.
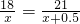
- D.
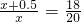
A
分析:首先设乙的速度为xkm/h,则甲的速度为(x+0.5)km/h,根据题意可知:甲行驶的路程=36÷2+2=20km,乙行驶的路程为18km,再根据甲乙两人行驶的时间相等可得方程: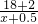 =
=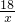 .
.
解答:设乙的速度为xkm/h,则甲的速度为(x+0.5)km/h,
由题意得: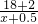 =
=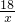 .
.
故选:A.
点评:此题主要考查了由实际问题抽象出分式方程,关键是理清甲乙两人所行驶的路程,再根据时间相等可得方程.
分析:首先设乙的速度为xkm/h,则甲的速度为(x+0.5)km/h,根据题意可知:甲行驶的路程=36÷2+2=20km,乙行驶的路程为18km,再根据甲乙两人行驶的时间相等可得方程:
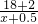 =
=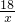 .
.解答:设乙的速度为xkm/h,则甲的速度为(x+0.5)km/h,
由题意得:
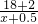 =
=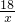 .
.故选:A.
点评:此题主要考查了由实际问题抽象出分式方程,关键是理清甲乙两人所行驶的路程,再根据时间相等可得方程.

练习册系列答案
相关题目