题目内容
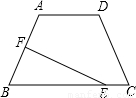
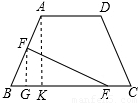
如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10.点E在下底边BC上,点F在腰AB上.
(1)若EF平分等腰梯形ABCD的周长,设BE长为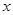 ,试用含
,试用含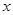 的代数式表示△BEF的面积;
的代数式表示△BEF的面积;
(2)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此BE的长;若不存在,请说明理由;
(3)是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1︰2的两部分?若存在,求此时BE的长;若不存在,请说明理由.
(1)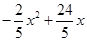 ;(2)BE=7;(3)不存在
;(2)BE=7;(3)不存在
【解析】
试题分析:(1)根据过点F作FG⊥BC于G,过点A作AK⊥BC于K,得出BF与FG的长即可求出;
(2)利用(1)中所求,解一元二次方程即可求出.
(3)仍然按照(1)和(2)的步骤和方法去做就可以了,注意不是分成相等的两份,而是1:2就可以了,得到关于x的一元二次方程,先求出根的判别式△,由于△<0,故不存在实数根.
(1)过点F作FG⊥BC于G,过点A作AK⊥BC于K,
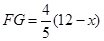
△BEF的面积为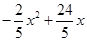 ;
;
(2)根据题意,得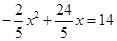
解得 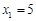 ,
,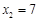 .
.
当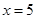 时,
时,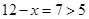 舍去;
舍去;
当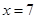 时,
时,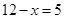 符合题意
符合题意
所以存在符合要求的线段EF,此时BE=7;
(3)假设存在线段EF将等腰梯形ABCD的周长和面积同时分成1:2的两部分.
∵等腰梯形ABCD的周长=24,等腰梯形ABCD的面积=28,AD+DC=9>8
∴只有BE+BF=8,△BEF的面积=
设BE长为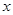 ,则
,则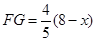 ,△BEF的面积
,△BEF的面积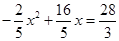
∵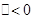 方程无解,
方程无解,
∴不存在线段EF将等腰梯形ABCD的周长和面积同时分成1︰2的两部分.
考点:本题主要考查了相似三角形的判定,根的判别式和解一元二次方程
点评:解答本题的关键是熟练掌握当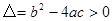 时,方程有两个不相等实数根;当
时,方程有两个不相等实数根;当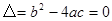 时,方程的两个相等的实数根;当
时,方程的两个相等的实数根;当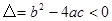 时,方程没有实数根。
时,方程没有实数根。

 在,求出这样的t的值;若不存在,请说明理由.
在,求出这样的t的值;若不存在,请说明理由. 10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE.
10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE. 已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD.
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD. (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
