题目内容
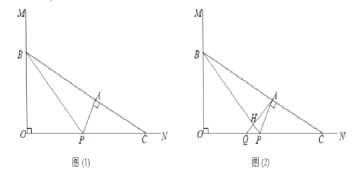
【题目】如图1,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 为
为![]() 的延长线上一点,
的延长线上一点,![]() 为半圆
为半圆![]() 的切线,切点为
的切线,切点为![]() .
.

(1)求证:![]() ;
;
(2)如图2,![]() 的平分线分别交
的平分线分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
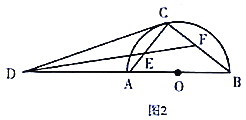
①求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①1;②![]()
【解析】
(1)连接![]() ,由切线性质得
,由切线性质得![]() ,根据直径所对的圆周角为直角得
,根据直径所对的圆周角为直角得![]() ,由“三角形中等角对等边”得
,由“三角形中等角对等边”得![]() ,根据角的等量代换即可证得
,根据角的等量代换即可证得![]() 。
。
(2)①根据角平分线性质和三角形外角性质进行角的等量代换即可得到![]() ,证得
,证得![]() 是等腰直角三角形,即可求得
是等腰直角三角形,即可求得![]() 的正切值。
的正切值。
②由勾股定理求得![]() ,通过
,通过![]() 得到线段比例式求得
得到线段比例式求得![]() 、
、![]() ,再由
,再由![]() 得到线段比例式求得
得到线段比例式求得![]() 即可。
即可。
(1)连接![]()
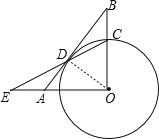
∵![]() 为半圆
为半圆![]() 切线∴
切线∴![]() ,即
,即![]()
∵![]() 为
为![]() 直径∴
直径∴![]() ∴
∴![]()
∵![]() ∴
∴![]() ∴
∴![]() ,即
,即![]()
(2)①∵![]() 是
是![]() 的平分线,∴
的平分线,∴![]()
∵![]() ,
,![]()
∵![]() ,即
,即![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]()
②在![]() 中,
中,![]() ,
,![]() ∴
∴![]()
∵![]() ,
,![]()
∴![]() ∴
∴![]()
设![]() ,
,![]() ,∴
,∴![]()
∵![]()
∴![]() ,即
,即![]() ∴
∴![]() (舍)
(舍)![]()
∴![]() ,
,![]() .
.
设![]() ,则
,则![]()
可得![]() ∴
∴![]()
即
![]()
∴![]()

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(![]() )请你根据表中的数据,写出一个符合p与x的函数表达式__________.
)请你根据表中的数据,写出一个符合p与x的函数表达式__________.
(![]() )农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?