题目内容
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
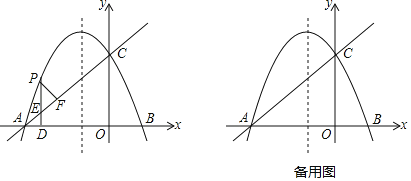
(1)求抛物线和直线l的解析式;
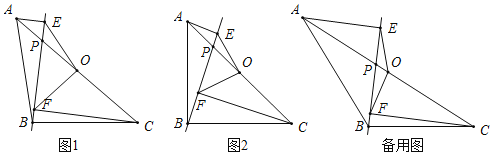
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)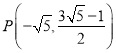 ;(3)存在,Q的坐标为:
;(3)存在,Q的坐标为: 或
或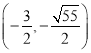
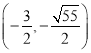 或
或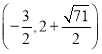 或
或 或
或![]() .
.
【解析】
(1)把点A、C的坐标和对称轴表达式代入二次函数表达式,即可求解;
(2)PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2,sin∠EAD=sin∠CAO,
n+2,sin∠EAD=sin∠CAO,![]() ,则AE
,则AE![]() DE
DE![]() (
(![]() n+2),当△PEF≌△AED时,PE=AE,
n+2),当△PEF≌△AED时,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),即可求解;
n+2),即可求解;
(3)等腰三角形分A为顶角顶点、以C为顶角顶点、点Q为顶角顶点,三种情况分别求解即可.
(1)把点A、C的坐标和对称轴表达式代入二次函数表达式得: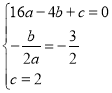 ,解得:
,解得: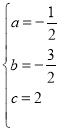 ,故抛物线的表达式为:y
,故抛物线的表达式为:y![]() x2
x2![]() x+2;
x+2;
同理把点A、C坐标代入直线l表达式并解得:y![]() x+2;
x+2;
(2)设P点坐标为(n,![]() n2
n2![]() n+2),∴E点坐标为(n,
n+2),∴E点坐标为(n,![]() n+2),∴PE
n+2),∴PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2.
n+2.
∵A(﹣4,0),C(0,2),OA=4,OC=2,AC=2![]() .
.
∵PD⊥x轴于点D,∴∠ADE=90°,∴sin∠EAD=sin∠CAO,![]() ,∴AE
,∴AE![]() DE
DE![]() (
(![]() n+2),当△PEF≌△AED时,PE=AE,
n+2),当△PEF≌△AED时,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),解得:n=﹣4或
n+2),解得:n=﹣4或![]() (舍去﹣4),∴n=
(舍去﹣4),∴n=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
(3)存在,理由如下:
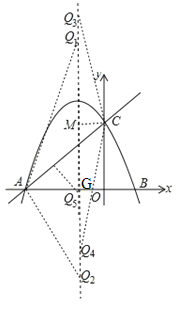
①以A为顶角顶点,AQ=AC,由(2)知AC=2![]() ,若设对称轴与x轴交于点G,则AG
,若设对称轴与x轴交于点G,则AG![]() (﹣4)
(﹣4)![]() ;
;
GQ1=GQ2![]() ,故点Q1、Q2的坐标分别为(
,故点Q1、Q2的坐标分别为(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
②以C为顶角顶点,CQ=CA=2![]() ,过点C作x轴的平行线,交抛物线的对称轴于点M,则M(
,过点C作x轴的平行线,交抛物线的对称轴于点M,则M(![]() ,2),则CM
,2),则CM![]() ,MQ3
,MQ3![]() ,Q3G=2
,Q3G=2![]() ,Q4G=﹣2
,Q4G=﹣2![]() ,故Q3、Q4坐标分别为(
,故Q3、Q4坐标分别为(![]() ,2
,2![]() )、(
)、(![]() ,2
,2![]() );
);
③以点Q为顶角顶点时,同理可得点Q5(![]() ,0);
,0);
故点Q的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,0).
,0).

【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如下表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
一般地,![]() 该种作物种子中大约有多少是不能发芽的?
该种作物种子中大约有多少是不能发芽的?