题目内容
(本小题满分8分)
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8)。
(1)求抛物线C1关于原点对称的抛物线C2的解析式;
(2)设抛物线C1的顶点为M,抛物线C2与x轴分别交于C、D两点(点C在点 D的左侧),顶点为N,四边形MDNA的面积为S。若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止。求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值;
(4)在运动过程中,四边形MDNA能否形成矩形?若能,求出此时t的值;若不能,请说明理由.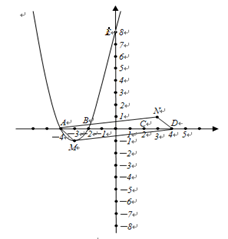
(1)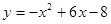
(2)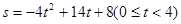
(3)当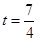 时,
时,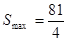 。
。
(4)在运动过程中MDNA可以形成矩形,此时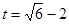
解析试题考查知识点:二次函数的解析式;中心对称图形;动点问题
思路分析:先求出抛物线C1的解析式,再根据中心对称图形的特点求抛物线C2的解析式;建立面积与时间的关系,再进行分析得出时间的变化范围;极值问题实际上是二次函数配方后的最大(小)值;根据矩形的判定方法建立关系,从而得解。
具体解答过程:
(1)、设抛物线C1的解析式为y=ax2+bx+c
∵抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8)
∴把x=-4,y=0与x=-2,y=0和x=0,y=8分别代入到解析式中,可得: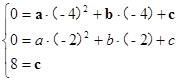 解之得:
解之得: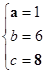
∴抛物线C1的解析式为y=x2+6x+8
如图所示,抛物线C1关于原点对称的抛物线C2的大致图像为: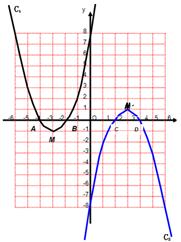
与抛物线C1的解析式为y=x2+6x+8比较可知,抛物线C2的解析式应为为-y=(-x)2+6(-x)+8即y=-x2+6x-8
(2)、如图所示。四边形MDNA的面积为S。若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动,直到点A与点D重合为止。可知A与D、M与N的运动各自具有对称性。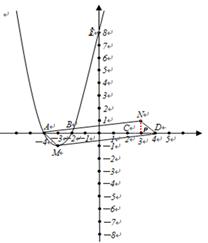
∵抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),抛物线C1与抛物线C2关于原点对称
∴C(2,0);D(4,0);N(0,1)且四边形MDNA的面积为S=2S△AND
做NP⊥x轴,垂足为P,则NP=1。当运动时间为t时,AD=8-2t,NP=1+2t
∴四边形MDNA的面积为S=2S△AND=2×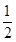 ×(8-2t)(1+2t)
×(8-2t)(1+2t)
即S=-4t2+14t+8
很显然,当A、D两点运动至原点位置处重合,此时,t=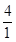 =4秒
=4秒
∴自变量t的取值范围为0≤t≤4
考虑到当t=4秒时,四边形MDNA将汇集成一条线段,故t=4秒应当舍去。
综上所述,四边形MDNA的面积S与运动时间t之间的关系式为S=-4t2+14t+8,且自变量t的取值范围为0≤t<4
(3)对于S=-4t2+14t+8,配方可得:S=-4(t-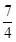 )2+
)2+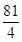
∵-4(t-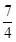 )2≤0
)2≤0
∴当t-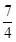 =0即t=
=0即t=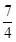 时,S有最大值,且最大值为
时,S有最大值,且最大值为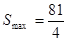
(4)在运动过程中,四边形MDNA能形成矩形。
当运动时间为t时,AD=8-2t,而的坐标为M(-3,-1-2t),N(3,1+2t)
∴此时线段MN的长度为MN= =2
=2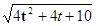
根据矩形的对角线相等的性质,当MN=AD时,四边形MDNA能形成矩形。
∴2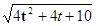 =8-2t解之得:t=±
=8-2t解之得:t=±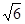 -2
-2
当t=-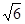 -2时,t<0,不符合题意,故舍去。
-2时,t<0,不符合题意,故舍去。
∴t=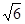 -2
-2
故知,在运动过程中,当t=-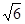 -2时,四边形MDNA能形成矩形。
-2时,四边形MDNA能形成矩形。
试题点评:这是一道关于二次函数、二元一次方程、根式方程、直角坐标系等的综合性试题。

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案



 不小于3cm吗?请说明理由.
不小于3cm吗?请说明理由. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的 ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的 .两根铁棒长度之和为55 cm.
.两根铁棒长度之和为55 cm.
 甲:
甲: 乙:
乙: =55
=55