题目内容
两边长分别为8cm、6cm的直角三角形的内切圆的半径长是 cm.
- A.2
- B.4
- C.
 -1
-1 - D.2或
 -1
-1
D
分析:设⊙O切AC于F,切BC于D,切AB于E,连接OA、OB、OC、OD、OE、OF,则OD=OE=OF,OD⊥BC,OF⊥AC,OE⊥AB,设OD=OE=OF=R,根据勾股定理求出第三边长,根据三角形的面积公式求出即可.
解答: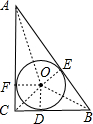 设⊙O切AC于F,切BC于D,切AB于E,连接OA、OB、OC、OD、OE、OF,
设⊙O切AC于F,切BC于D,切AB于E,连接OA、OB、OC、OD、OE、OF,
则OD=OE=OF,OD⊥BC,OF⊥AC,OE⊥AB,
设OD=OE=OF=R,
分为两种情况:①当AC=8,BC=6时,由勾股定理得:AB= =10,
=10,
∵S△ACB=S△OAC+S△OBC+S△OAB,
∴ AC×BC=
AC×BC= AC×OF+
AC×OF+ BC×OD+
BC×OD+ AB×OE,
AB×OE,
即8×6=8R+6R+10R,
R=2;
②当AB=8,BC=6时,由勾股定理得:AC=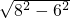 =2
=2 ,
,
∵S△ACB=S△OAC+S△OBC+S△OAB,
∴ AC×BC=
AC×BC= AC×OF+
AC×OF+ BC×OD+
BC×OD+ AB×OE,
AB×OE,
即2 ×6=2
×6=2 R+8R+6R,
R+8R+6R,
R= -1;
-1;
故选D.
点评:本题考查了三角形的内切圆与内心,勾股定理,三角形的面积,切线的性质等知识点,注意:①要进行分类讨论,②利用三角形的面积相等求出R比较好.
分析:设⊙O切AC于F,切BC于D,切AB于E,连接OA、OB、OC、OD、OE、OF,则OD=OE=OF,OD⊥BC,OF⊥AC,OE⊥AB,设OD=OE=OF=R,根据勾股定理求出第三边长,根据三角形的面积公式求出即可.
解答:
 设⊙O切AC于F,切BC于D,切AB于E,连接OA、OB、OC、OD、OE、OF,
设⊙O切AC于F,切BC于D,切AB于E,连接OA、OB、OC、OD、OE、OF,则OD=OE=OF,OD⊥BC,OF⊥AC,OE⊥AB,
设OD=OE=OF=R,
分为两种情况:①当AC=8,BC=6时,由勾股定理得:AB=
 =10,
=10,∵S△ACB=S△OAC+S△OBC+S△OAB,
∴
 AC×BC=
AC×BC= AC×OF+
AC×OF+ BC×OD+
BC×OD+ AB×OE,
AB×OE,即8×6=8R+6R+10R,
R=2;
②当AB=8,BC=6时,由勾股定理得:AC=
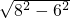 =2
=2 ,
,∵S△ACB=S△OAC+S△OBC+S△OAB,
∴
 AC×BC=
AC×BC= AC×OF+
AC×OF+ BC×OD+
BC×OD+ AB×OE,
AB×OE,即2
 ×6=2
×6=2 R+8R+6R,
R+8R+6R,R=
 -1;
-1;故选D.
点评:本题考查了三角形的内切圆与内心,勾股定理,三角形的面积,切线的性质等知识点,注意:①要进行分类讨论,②利用三角形的面积相等求出R比较好.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目