题目内容
如图已知直线L:y=| 3 | 4 |
(1)求点A、点B的坐标.
(2)设F为x轴上一动点,用尺规作图作出⊙P,使⊙P经过点B且与x轴相切于点F(不写作法,保留作图痕迹).
(3)设(2)中所作的⊙P的圆心坐标为P(x,y),求y关于x的函数关系式.
(4)是否存在这样的⊙P,既与x轴相切又与直线L相切于点B?若存在,求出圆
 心P的坐标;若不存在,请说明理由.
心P的坐标;若不存在,请说明理由.
分析:(1)令x=0以及y=0代入直线解析式可求出A,B的坐标;
(2)做PD⊥y轴于D,根据勾股定理得出PB2=PD2+BD2,BP2=PD2+BD2.得出y与x的关系式即可;
(3)依题意可得AB2=OA2+OB2=AF2=52,求出关于x的值代入解析式,求出y值即可,求出点P的坐标.
(2)做PD⊥y轴于D,根据勾股定理得出PB2=PD2+BD2,BP2=PD2+BD2.得出y与x的关系式即可;
(3)依题意可得AB2=OA2+OB2=AF2=52,求出关于x的值代入解析式,求出y值即可,求出点P的坐标.
解答: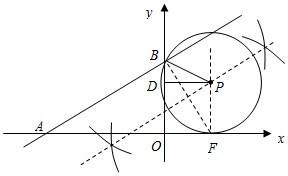 解:(1)令y=0得x=-4,令x=0得,y=3,
解:(1)令y=0得x=-4,令x=0得,y=3,
∴A(-4,0),B(0,3);
(2)如图:
(3)过点P作PD⊥y轴于D,则PD=|x|,BD=|3-y|,PB=PF=y,
∵△BDP为直角三角形,
∴BP2=PD2+BD2,
即|y|2=|x|2+|3-y|2,
y2=x2+(3-y)2,
∴y与x的函数关系为y=
x2+
;
(4)存在.
解:∵⊙P与x轴相切于点F,且与直线l相切于点B,
∴AB=AF,
∵AB2=OA2+OB2=52,
∴AF2=52,
∵AF=|x+4|,
∴(x+4)2=52,
∴x=1或x=-9,
把x=1或x=-9代入y=
x2+
,
得y=
或y=15,
∴点P的坐标为(1,
)或(-9,15).
 解:(1)令y=0得x=-4,令x=0得,y=3,
解:(1)令y=0得x=-4,令x=0得,y=3,∴A(-4,0),B(0,3);
(2)如图:
(3)过点P作PD⊥y轴于D,则PD=|x|,BD=|3-y|,PB=PF=y,
∵△BDP为直角三角形,
∴BP2=PD2+BD2,
即|y|2=|x|2+|3-y|2,
y2=x2+(3-y)2,
∴y与x的函数关系为y=
| 1 |
| 6 |
| 3 |
| 2 |
(4)存在.
解:∵⊙P与x轴相切于点F,且与直线l相切于点B,
∴AB=AF,
∵AB2=OA2+OB2=52,
∴AF2=52,
∵AF=|x+4|,
∴(x+4)2=52,
∴x=1或x=-9,
把x=1或x=-9代入y=
| 1 |
| 6 |
| 3 |
| 2 |
得y=
| 5 |
| 3 |
∴点P的坐标为(1,
| 5 |
| 3 |
点评:本题考查的是一次函数的图形与应用的有关知识以及考生作图能力,难度中等.

练习册系列答案
相关题目

 AB.
AB.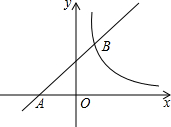 如图已知直线y=kx+b与x轴交于A点,且与函数
如图已知直线y=kx+b与x轴交于A点,且与函数 如图已知直线a,b相交,∠1+∠2=280°,则∠2=
如图已知直线a,b相交,∠1+∠2=280°,则∠2=