题目内容
【题目】已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC. 
【答案】证明:如图所示,∵HF⊥AB,CD⊥AB, ∴CD∥HF,
∴∠2+∠3=180°,
又∵∠1与∠2互补,
∴∠2+∠1=180°,
∴∠1=∠3,
∴DE∥BC,
∵AC⊥BC,
∴DE⊥AC.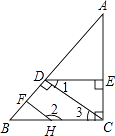
【解析】根据AC⊥BC,DE⊥AC,易证DE∥BC,那么∠2+∠3=180°,而∠1与∠2互补,从而可证∠1=∠3,即可得出DE∥BC,结合AC⊥BC,易得DE⊥AC.
【考点精析】通过灵活运用余角和补角的特征和平行线的判定与性质,掌握互余、互补是指两个角的数量关系,与两个角的位置无关;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质即可以解答此题.

练习册系列答案
相关题目
【题目】我市某西瓜产地组织40辆汽车装运完A,B,C三种西瓜共200吨到外地销售.按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满.根据下表提供的信息,解答以下问题:
西瓜种类 | A | B | C |
每辆汽车运载量(吨) | 4 | 5 | 6 |
每吨西瓜获利(百元) | 16 | 10 | 12 |
(1)设装运A种西瓜的车辆数为x辆,装运B种西瓜的车辆数为y辆,求y与x的函数关系式;
(2)如果装运每种西瓜的车辆数都不少于10辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要是此次销售获利达到预期利润25万元,应采取怎样的车辆安排方案?