题目内容
在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).(1)用列表法或树形图表示出(x,y)的所用可能出现的结果;
(2)求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率.
分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果即可.
(2)从数对中找出方程x+y=5的解,然后根据概率公式求出该事件的概率即可解答.
(2)从数对中找出方程x+y=5的解,然后根据概率公式求出该事件的概率即可解答.
解答:解:(1)出现的情况如下:
一共有16种.
(2)数对(2,3),(3,2)是方程x+y=5的解,所以P(和等于5)=
=
.
| 红桃2 | 红桃3 | 红桃4 | 红桃5 | |
| 红桃2 | 2,2 | 2,3 | 2,4 | 2,5 |
| 红桃3 | 3,2 | 3,3 | 3,4 | 3,5 |
| 红桃4 | 4,2 | 4,3 | 4,4 | 4,5 |
| 红桃5 | 5,2 | 5,3 | 5,4 | 5,5 |
(2)数对(2,3),(3,2)是方程x+y=5的解,所以P(和等于5)=
| 2 |
| 16 |
| 1 |
| 8 |
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
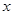 ,然后放回洗匀,再由小华随机摸出一张,记下牌面上的数字为
,然后放回洗匀,再由小华随机摸出一张,记下牌面上的数字为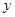 ,组成一对数(
,组成一对数(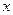 ,然后放回洗匀,再由小华随机摸出一张,记下牌面上的数字为
,然后放回洗匀,再由小华随机摸出一张,记下牌面上的数字为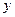 ,组成一对数(
,组成一对数(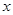 ,然后放回洗匀,再由小华随机摸出一张,记下牌面上的数字为
,然后放回洗匀,再由小华随机摸出一张,记下牌面上的数字为 ,组成一对数(
,组成一对数(