题目内容
【题目】在平面直角坐标系中，点M的坐标为
，点N的坐标为
，点P为抛物线
上的一个动点，当
之长最短时点P的坐标是________.
【答案】（0，2）
【解析】
如图所示，连接MN，与抛物线交于P点，根据两点之间线段最短得到此时PM+PN最短，设直线MN的解析式为y=kx+b，将M与N坐标代入得到关于k与b的方程组，求出方程组的解得到k与b的值，确定出直线MN解析式，与抛物线解析式联立组成方程组，求出方程组的解得到x与y的值，即可确定出此时P的坐标．
连接MN，与抛物线交于P点，此时PM+PN最短，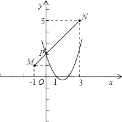
设直线MN的解析式为y=kx+b，
将M(1,1),N(3,5)代入得：
解得：
故直线MN解析式y=x+2，
与抛物线解析式联立得：
解得：
则此时P的坐标为(0,2).
练习册系列答案
阳光课堂课时作业系列答案
相关题目
