题目内容
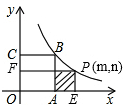 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=| k |
| x |
| k |
| x |
(1)求B点的坐标和k的值;
(2)当S=
| 8 |
| 3 |
(3)写出S关于m的函数关系式.
分析:(1)利用正方形的性质得OA=AB=2,则B点坐标为(2,2);把B(4,4)代入y=
中,即可求出k;
(2)分类:P(m,n)在y=
上,得到mn=4,当x>2,S=AE•PE=(m-2)•n=mn-2n=4-2n=
,解得n=
;当0<x≤2,S=P′F′•F′C=m(n-2)=mn-2m=4-2m=
,解得m=
,即可确定P点坐标;
(3)由(2)得易得到S关于m的函数关系式:当x>2,S=(m-2)•n,当0<x≤2,S=m(n-2).
| k |
| x |
(2)分类:P(m,n)在y=
| 4 |
| x |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
(3)由(2)得易得到S关于m的函数关系式:当x>2,S=(m-2)•n,当0<x≤2,S=m(n-2).
解答: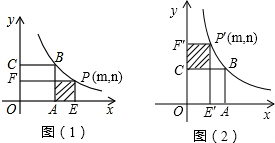 解:(1)∵正方形OABC的面积为4,即OA=AB=2,
解:(1)∵正方形OABC的面积为4,即OA=AB=2,
∴B点坐标为(2,2);
把B(2,2)代入y=
中,得k=2×2=4;
所以B点的坐标为(2,2),k的值为4;
(2)如图,
∵P(m,n)在y=
上,
∴mn=4,
当x>2,
∴S=AE•PE=(m-2)•n=mn-2n=4-2n=
,
解得n=
,则m=6,
∴P点坐标为(6,
);
当0<x≤2,
∴S=P′F′•F′C=m(n-2)=mn-2m=4-2m=
,
解得m=
,则n=6,
∴P′点坐标为(
,6);
所以点P的坐标为(6,
)或(
,6);
(3)由(2)得
当x>2,S=(m-2)•n=mn-2n=4-2•
=
;
当0<x≤2,S=m(n-2)=mn-2m=4-2m.
 解:(1)∵正方形OABC的面积为4,即OA=AB=2,
解:(1)∵正方形OABC的面积为4,即OA=AB=2,∴B点坐标为(2,2);
把B(2,2)代入y=
| k |
| x |
所以B点的坐标为(2,2),k的值为4;
(2)如图,
∵P(m,n)在y=
| 4 |
| x |
∴mn=4,
当x>2,
∴S=AE•PE=(m-2)•n=mn-2n=4-2n=
| 8 |
| 3 |
解得n=
| 2 |
| 3 |
∴P点坐标为(6,
| 2 |
| 3 |
当0<x≤2,
∴S=P′F′•F′C=m(n-2)=mn-2m=4-2m=
| 8 |
| 3 |
解得m=
| 2 |
| 3 |
∴P′点坐标为(
| 2 |
| 3 |
所以点P的坐标为(6,
| 2 |
| 3 |
| 2 |
| 3 |
(3)由(2)得
当x>2,S=(m-2)•n=mn-2n=4-2•
| 4 |
| m |
| 4m-8 |
| m |
当0<x≤2,S=m(n-2)=mn-2m=4-2m.
点评:本题考查了反比例函数的综合题的解法:先利用待定系数法确定反比例的解析式,那么图象上所有点的横纵坐标的乘积为定值.也考查了矩形的性质以及分类讨论思想的运用.

练习册系列答案
相关题目

 如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=
如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y= 如图所示,已知正方形OABC的面积为9,点B在函数
如图所示,已知正方形OABC的面积为9,点B在函数