ЬтФПФкШн
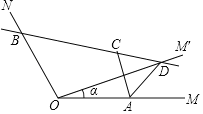
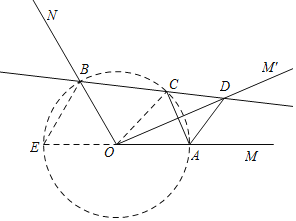
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯMON=120ЁуЃЌЕуAЃЌBЗжБ№дкOMЃЌONЩЯЃЌЧвOA=OB=aЃЌНЋЩфЯпOMШЦЕуOФцЪБеыа§зЊЕУЕНOMЁфЃЌа§зЊНЧЮЊІСЃЈ0ЁуЃМІСЃМ120ЁуЧвІСЁй60ЁуЃЉЃЌзїЕуAЙигкжБЯпOMЁфЕФЖдГЦЕуCЃЌЛжБЯпBCНЛOMЁфгкЕуDЃЌСЌНгACЃЌADЃЌгаЯТСаНсТлЃК
ЂйAD=CDЃЛ
ЂкЁЯACDЕФДѓаЁЫцзХІСЕФБфЛЏЖјБфЛЏЃЛ
ЂлЕБІС=30ЁуЪБЃЌЫФБпаЮOADCЮЊСтаЮЃЛ
ЂмЁїACDУцЛ§ЕФзюДѓжЕЮЊ![]() a2ЃЛ
a2ЃЛ
Цфжае§ШЗЕФЪЧ_____ЃЎЃЈАбФуШЯЮЊе§ШЗНсТлЕФађКХЖМЬюЩЯЃЉЃЎ
ЁОД№АИЁПЂйЂлЂм
ЁОНтЮіЁПЂйИљОнЖдГЦЕФаджЪЃКЖдГЦЕуЕФСЌЯпБЛЖдГЦжсДЙжБЦНЗжПЩЕУЃКOM'ЪЧACЕФДЙжБЦНЗжЯпЃЌдйгЩДЙжБЦНЗжЯпЕФаджЪПЩзїХаЖЯЃЛ
ЂквдOЮЊдВаФЃЌвдOAЮЊАыОЖзїЁбOЃЌНЛAOЕФбгГЄЯпгкEЃЌСЌНгBEЃЌдђAЁЂBЁЂCЖМдкЁбOЩЯЃЌИљОнЫФЕуЙВдВЕФаджЪЕУЃКЁЯACD=ЁЯE=60ЁуЃЌЫЕУїЁЯACDЪЧЖЈжЕЃЌВЛЛсЫцзХІСЕФБфЛЏЖјБфЛЏЃЛ
ЂлЕБІС=30ЁуЪБЃЌМДЁЯAOD=ЁЯCOD=30ЁуЃЌжЄУїЁїAOCЪЧЕШБпШ§НЧаЮКЭЁїACDЪЧЕШБпШ§НЧаЮЃЌЕУOC=OA=AD=CDЃЌПЩзїХаЖЯЃЛ
ЂмЯШжЄУїЁїACDЪЧЕШБпШ§НЧаЮЃЌЕБACзюДѓЪБЃЌЁїACDЕФУцЛ§зюДѓЃЌЕБACЮЊжБОЖЪБзюДѓЃЌИљОнУцЛ§ЙЋЪНМЦЫуКѓПЩзїХаЖЯЃЎ
ЂйЁпAЁЂCЙигкжБЯпOM'ЖдГЦЃЌ
ЁрOM'ЪЧACЕФДЙжБЦНЗжЯпЃЌ
ЁрCD=ADЃЌЙЪЂйе§ШЗЃЛ
ЂкСЌНгOCЃЌ
гЩЂйжЊЃКOM'ЪЧACЕФДЙжБЦНЗжЯпЃЌЁрOC=OAЃЌ
ЁрOA=OB=OCЃЌ
вдOЮЊдВаФЃЌвдOAЮЊАыОЖзїЁбOЃЌНЛAOЕФбгГЄЯпгкEЃЌСЌНгBEЃЌ
дђAЁЂBЁЂCЖМдкЁбOЩЯЃЌ
ЁпЁЯMON=120ЁуЃЌ
ЁрЁЯBOE=60ЁуЃЌ
ЁпOB=OEЃЌ
ЁрЁїOBEЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯE=60ЁуЃЌ
ЁпAЁЂCЁЂBЁЂEЫФЕуЙВдВЃЌ
ЁрЁЯACD=ЁЯE=60ЁуЃЌЙЪЂкВЛе§ШЗЃЛ
ЂлЕБІС=30ЁуЪБЃЌМДЁЯAOD=ЁЯCOD=30ЁуЃЌ
ЁрЁЯAOC=60ЁуЃЌ
ЁрЁїAOCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯOAC=60ЁуЃЌOC=OA=ACЃЌ
гЩЂйЕУЃКCD=ADЃЌ
ЁрЁЯCAD=ЁЯACD=ЁЯCDA=60ЁуЃЌ
ЁрЁїACDЪЧЕШБпШ§НЧаЮЃЌ
ЁрAC=AD=CDЃЌ
ЁрOC=OA=AD=CDЃЌ
ЁрЫФБпаЮOADCЮЊСтаЮЃЌЙЪЂле§ШЗЃЛ
ЂмЁпCD=ADЃЌЁЯACD=60ЁуЃЌ
ЁрЁїACDЪЧЕШБпШ§НЧаЮЃЌ
ЕБACзюДѓЪБЃЌЁїACDЕФУцЛ§зюДѓЃЌ
ЁпACЪЧЁбOЕФЯвЃЌМДЕБACЮЊжБОЖЪБзюДѓЃЌДЫЪБAC=2OA=2aЃЌІС=90ЁуЃЌ
ЁрЁїACDУцЛ§ЕФзюДѓжЕЪЧЃК![]() AC2=
AC2=![]() ЃЌЙЪЂме§ШЗЃЌ
ЃЌЙЪЂме§ШЗЃЌ
ЫљвдБОЬтНсТле§ШЗЕФгаЃКЂйЂлЂмЃЌ
ЙЪД№АИЮЊЃКЂйЂлЂмЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ