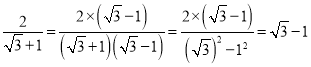题目内容
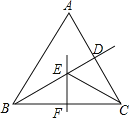
【题目】如图,正方形ABCD的边长为2,E在正方形外,![]() ,过D作
,过D作![]() 于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
①![]() ;②
;②![]() ;③
;③![]() ;④若PD=3AD,则MD=
;④若PD=3AD,则MD=![]()
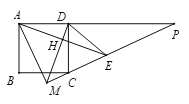
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的性质,利用全等的判定和性质、相似的判定和性质、垂直平分线的判定性质、勾股定理等知识对四个结论一一判断即可.
在正方形ABCD中,
AD=DC,
∵DE=DC,
∴AD=DE,
∴∠DAE=∠DEA,
∴①正确;
∵AD=DE,DH⊥AE,
∴DM是AE的垂直平分线,
∴AM=EM,
∴△AMD≌△EMD,
∴∠MAD=∠MED,
∵DE=DC,
∴∠DCE=∠MED,
∴∠MAD=∠DCE,
即∠MAH+∠DAH=∠DME+∠CDM
∵∠DAH+∠ADH=90°,
∠CDM+∠ADH=90°,
∴∠DAH=∠CDM,
∴∠MAH=∠DME,
∵AM=EM,
∴∠MAH=∠MEH,
∴∠DME=∠MEH,
∵DH⊥AE,
∴∠DME=∠MEH=45°,
故②正确;
在EP上截取EN=MC,则△DCM≌△DEN,
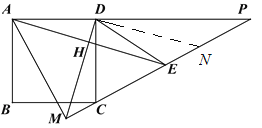
∴∠DNM=∠DME=45°,
∴△DMN是等腰直角三角形,
∴![]() ,
,
∵MN=ME+EN=AM+MC,
∴![]() ,
,
故③正确;
∵PD=3AD,AD=2,
∴PD=6,PA=8,
∵DM是AE的垂直平分线,
且∠DME=45°,
∴∠AMP=90°,
∴△PDC∽△PMA,
∴![]() ,
,
在Rt△PDC中, PC=![]() =2
=2![]() ,
,
在Rt△PAM中,AM=![]() ,PM=
,PM=![]() ,
,
∴CM=![]() ,
,
∵![]() ,
,
∴DM=![]() =
=![]() .
.
故④错误.
故选C.

练习册系列答案
相关题目