题目内容
如图,直线AB∥CD.
(1)在图1中,∠BME、∠E,∠END的数量关系为:
在图2中,∠BMF、∠F,∠FND的数量关系为:
(2)如图3,NE平分∠FND,MB平分∠FME,且2∠E与∠F互补,求∠FME的大小.
(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,EQ∥NP,则∠FEQ的大小是否发生变化?若变化,说明理由;若不变化,求∠FEQ的度数.
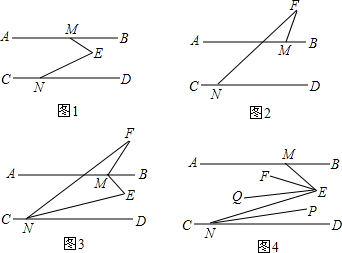
(1)在图1中,∠BME、∠E,∠END的数量关系为:
∠E=∠BME+∠END
∠E=∠BME+∠END
;(不需证明)在图2中,∠BMF、∠F,∠FND的数量关系为:
∠BMF=∠F+∠FND
∠BMF=∠F+∠FND
;(不需证明)(2)如图3,NE平分∠FND,MB平分∠FME,且2∠E与∠F互补,求∠FME的大小.
(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,EQ∥NP,则∠FEQ的大小是否发生变化?若变化,说明理由;若不变化,求∠FEQ的度数.

分析:(1)过点E作EF∥AB,根据两直线平行,内错角相等可得∠BME=∠1,∠END=∠2,然后相加即可得解;先根据两直线平行,同位角相等求出∠3=∠FND,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)设∠END=x°,∠BNE=y°,根据(1)的结论可得x+y=∠E,2x+∠F=y,然后消掉x并表示出y,再根据2∠E与∠F互补求出y,然后根据角平分线的定义求解即可;
(3)根据(1)的结论表示出∠MEN,再根据角平分线的定义表示出∠FEN和∠ENP,再根据两直线平行,内错角相等可得∠NEQ=∠ENP,然后根据∠FEQ=∠FEN-∠NEQ整理即可得解.
(2)设∠END=x°,∠BNE=y°,根据(1)的结论可得x+y=∠E,2x+∠F=y,然后消掉x并表示出y,再根据2∠E与∠F互补求出y,然后根据角平分线的定义求解即可;
(3)根据(1)的结论表示出∠MEN,再根据角平分线的定义表示出∠FEN和∠ENP,再根据两直线平行,内错角相等可得∠NEQ=∠ENP,然后根据∠FEQ=∠FEN-∠NEQ整理即可得解.
解答:解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠BME=∠1,∠END=∠2,
∴∠1+∠2=∠BME+∠END,
即∠E=∠BME+∠END;
如图2,∵AB∥CD,
∴∠3=∠FND,
∴∠BMF=∠F+∠3=∠F+∠FND,
即∠BMF=∠F+∠FND;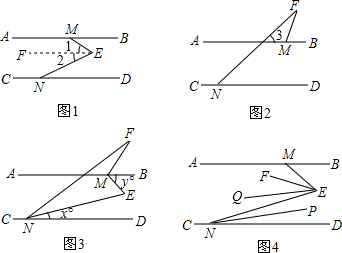
故答案为:∠E=∠BME+∠END;∠BMF=∠F+∠FND;
(2)如图3,设∠END=x°,∠BNE=y°,
由(1)的结论可得x+y=∠E,2x+∠F=y,
消掉x得,3y=2∠E+∠F,
∵2∠E与∠F互补,
∴2∠E+∠F=180°,
∴3y=180°,
解得y=60°,
∵MB平分∠FME,
∴∠FME=2y=2×60°=120°;
(3)由(1)的结论得,∠MEN=∠BME+∠END,
∵EF平分∠MEN,NP平分∠END,
∴∠FEN=
∠MEN=
(∠BME+∠END),
∠ENP=
∠END,
∵EQ∥NP,
∴∠NEQ=∠ENP,
∴∠FEQ=∠FEN-∠NEQ=
(∠BME+∠END)-
∠END=
∠BME,
∵∠BME=60°,
∴∠FEQ=
×60°=30°.
∵AB∥CD,
∴AB∥EF∥CD,
∴∠BME=∠1,∠END=∠2,
∴∠1+∠2=∠BME+∠END,
即∠E=∠BME+∠END;
如图2,∵AB∥CD,
∴∠3=∠FND,
∴∠BMF=∠F+∠3=∠F+∠FND,
即∠BMF=∠F+∠FND;

故答案为:∠E=∠BME+∠END;∠BMF=∠F+∠FND;
(2)如图3,设∠END=x°,∠BNE=y°,
由(1)的结论可得x+y=∠E,2x+∠F=y,
消掉x得,3y=2∠E+∠F,
∵2∠E与∠F互补,
∴2∠E+∠F=180°,
∴3y=180°,
解得y=60°,
∵MB平分∠FME,
∴∠FME=2y=2×60°=120°;
(3)由(1)的结论得,∠MEN=∠BME+∠END,
∵EF平分∠MEN,NP平分∠END,
∴∠FEN=
| 1 |
| 2 |
| 1 |
| 2 |
∠ENP=
| 1 |
| 2 |
∵EQ∥NP,
∴∠NEQ=∠ENP,
∴∠FEQ=∠FEN-∠NEQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BME=60°,
∴∠FEQ=
| 1 |
| 2 |
点评:本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,此类题目,过拐点作平行线是解题的关键,准确识图理清图中各角度之间的关系也很重要.

练习册系列答案
相关题目
 22、如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,FH平分∠EFD,若∠FEH=110°,求∠EHF的度数.
22、如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,FH平分∠EFD,若∠FEH=110°,求∠EHF的度数. 2、如图,直线AB∥CD,EF⊥AB于E,交CD于F,直线MN交AB于M,CD于N,EF于O,则直线AB和CD之间的距离是哪个线段的长( )
2、如图,直线AB∥CD,EF⊥AB于E,交CD于F,直线MN交AB于M,CD于N,EF于O,则直线AB和CD之间的距离是哪个线段的长( ) 9、如图,直线AB∥CD,∠A=45°,∠C=125°,则∠E=
9、如图,直线AB∥CD,∠A=45°,∠C=125°,则∠E= 14、如图,直线AB∥CD,∠PQA=25°,∠PRC=60°,则∠P=
14、如图,直线AB∥CD,∠PQA=25°,∠PRC=60°,则∠P= (2012•高安市二模)如图,直线AB∥CD,GH与AB、CD分别交于点M、F,若∠GMB=70°,∠CEF=50°,则∠C=
(2012•高安市二模)如图,直线AB∥CD,GH与AB、CD分别交于点M、F,若∠GMB=70°,∠CEF=50°,则∠C=