题目内容
(1)若方程mx+ny=6的两个解是
|
|
(2)解不等式
| x+1 |
| 6 |
| 2x-5 |
| 4 |
(3)解不等式组
|
分析:(1)分别把
和
代入方程mx+ny=6,得到关于m、n的方程组,求出m、n的值即可;
(2)先把原不等式去分母、去括号,再移项、合并同类项、化系数为1,即可求出不等式的解集,在数轴上表示出来即可;
(3)先求出不等式的解集,再求出符合条件的整数解即可.
|
|
(2)先把原不等式去分母、去括号,再移项、合并同类项、化系数为1,即可求出不等式的解集,在数轴上表示出来即可;
(3)先求出不等式的解集,再求出符合条件的整数解即可.
解答:解:(1)把
和
代入方程mx+ny=6得
,
①+②得,3m=12,m=4;
把m=4代入①得,4+n=6,解得.n=2.
故原方程组的解为
.
(2)不等式两边同乘以12得,2(x+1)<3(2x-5)+12,
去括号、移项、合并同类项得,-4x<-5,
化系数为1得,x>
.
在数轴上表示为:
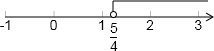
(3)原不等式组可化为
,解得1≤x<3.
故其整数解为1、2,共两个.
|
|
|
①+②得,3m=12,m=4;
把m=4代入①得,4+n=6,解得.n=2.
故原方程组的解为
|
(2)不等式两边同乘以12得,2(x+1)<3(2x-5)+12,
去括号、移项、合并同类项得,-4x<-5,
化系数为1得,x>
| 5 |
| 4 |
在数轴上表示为:

(3)原不等式组可化为
|
故其整数解为1、2,共两个.
点评:此题综合考查了二元一次方程组、一元一次不等式及二元一次不等式组的解法,具有一定的综合性,但难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若方程mx-2y=2的一组解是
,则m的值是( )
|
A、
| ||
B、
| ||
| C、4 | ||
D、-
|