题目内容
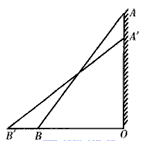
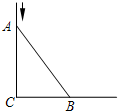 如图,长为10米的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8米.
如图,长为10米的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8米.(1)如果梯子的顶端下滑2米,那么它的底端滑动多少米?
(2)你认为梯子顶端下滑的高度与它的底端滑动的长度一定相等吗?若相等,请说明理由;若不相等,请举例说明.
分析:(1)利用勾股定理求出BC及B'C的长度,即可得出底端滑动的距离.
(2)顶端下滑的高度与底端滑动的长度不一定相等,举一例说明即可.
(2)顶端下滑的高度与底端滑动的长度不一定相等,举一例说明即可.
解答:解:(1)下滑前BC=
=
=6米,
下滑后B'C=
=
=8米,
故底端滑动2米.
(2)不一定.
如顶端下滑1米,底端滑动不是1米(答案不唯一).
| AB2-BC2 |
| 102-82 |
下滑后B'C=
| AB2-A′C2 |
| 102-62 |
故底端滑动2米.
(2)不一定.
如顶端下滑1米,底端滑动不是1米(答案不唯一).
点评:本题考查了勾股定理的应用,属于基础题,熟练掌握勾股定理的表达式是解答此类题目的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
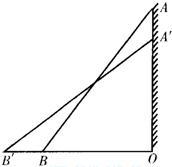 15、如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯
15、如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯
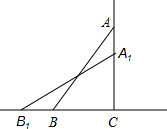 如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米,那么它的底端滑动多少米?如果梯子的顶端沿墙下滑2米,那么梯足将向外移多少米?
如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米,那么它的底端滑动多少米?如果梯子的顶端沿墙下滑2米,那么梯足将向外移多少米?
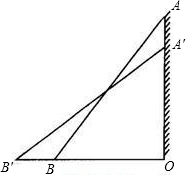 如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯________米.
如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯________米.