题目内容
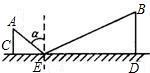 如图所示,CD是平面镜,光线从A点出发经CD上的E点反射后到达B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值是( )
如图所示,CD是平面镜,光线从A点出发经CD上的E点反射后到达B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:首先α不在直角三角形中,所以先找一个和α相等的角,因为AC、BD、法线均和镜面垂直,所以∠A=∠B=α,因为△ACE∽△BDE,所以
=
,由此可以求出CE,然后在三角形ACE中tanA=tanα可以求出tanα的值.
| CE |
| DE |
| AC |
| BD |
解答:解:因为AC、BD、法线均和镜面垂直,
所以∠A=∠B=α,
而由已知得△ACE∽△BDE,
所以
=
即
=
∴CE=
,
在三角形ACE中tanA=
=
=
=tanα.
故选D.
所以∠A=∠B=α,
而由已知得△ACE∽△BDE,
所以
| CE |
| DE |
| AC |
| BD |
| CE |
| 11-CE |
| 3 |
| 6 |
∴CE=
| 11 |
| 3 |
在三角形ACE中tanA=
| CE |
| AC |
| ||
| 3 |
| 11 |
| 9 |
故选D.
点评:解此题的关键是角之间的转化,把实际问题转化为数学问题,利用正切的定义解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 部分为一段抛物线,顶点G的高度为8米,AD和
部分为一段抛物线,顶点G的高度为8米,AD和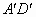 是两侧高为5.5米的支柱,OA和
是两侧高为5.5米的支柱,OA和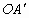 为两个方向的汽车通行区,宽都为15米,线段CD和
为两个方向的汽车通行区,宽都为15米,线段CD和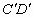 为两段对称的上桥斜坡,其坡度1:4.
为两段对称的上桥斜坡,其坡度1:4.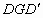 所在抛物线的关系式及
所在抛物线的关系式及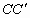 的长;
的长;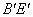 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和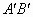 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和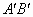 的宽;
的宽;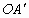 )区域安全通过?请说明理由.
)区域安全通过?请说明理由.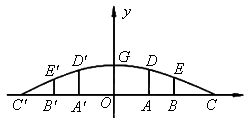
 ),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)
),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)
 ),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)
),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)