题目内容
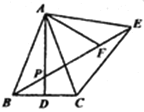
【题目】如图,在![]() 中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
中,AB=AC,AD是BC边的中线,以AC为边作等边△ACE,BE与AD相交于点P,点F在BE上,且PF=PA,连接AF下列四个结论:①AD⊥BC;②∠ABE=∠AEB;③∠APE=60°;④△AEF≌△ABP,其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由等腰三角形“三线合一”的性质可得AD⊥BC,∠BAD=∠CAD,可对①进行判断;由AB=AC,△ACE是等边三角形可得AB=AE,根据等腰三角形的性质可得∠ABE=∠AEB,可对②进行判断;由三角形内角和定理可得∠ABE+∠AEB+∠BAD+∠CAD+∠CAE=180°,即可求出∠BAD+∠ABE=60°,根据外角性质可得∠APE=∠BAD+∠ABE=60°,可对③进行判断;由AP=PF,∠APE=60°可得△APF是等边三角形,可得∠APB=∠AFE=120°,利用AAS即可证明△AEF≌△ABP,可对④进行判断;综上即可得答案.
∵AB=AC,AD是BC边中线,
∴∠BAD=∠CAD,AD⊥BC,故①正确,
∵△ACE是等边三角形,
∴AC=AE,∠CAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,故②正确,
∵∠ABE+∠AEB+∠BAE=180°,
∴∠ABE+∠AEB+∠BAD+∠CAD+∠CAE=180°,即2(∠BAD+∠ABE)+60°=180°,
∴∠ABE+∠BAD=60°,
∴∠APE=∠ABE+∠BAD=60°,故③正确,
∵AP=PF,∠APE=60°,
∴△APF是等边三角形,
∴∠APF=∠AFP=60°,
∴∠APB=∠AFE=120°,
在△AEF和△ABP中,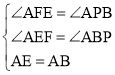 ,
,
∴△AEF≌△ABP,故④正确,
综上所述:正确的结论有①②③④,共4个,
故选:D.

练习册系列答案
相关题目



