题目内容
(2012•高邮市一模)如图,一根电线杆AB和一块半圆形广告牌在太阳照射下,顶端A的影子刚好落在半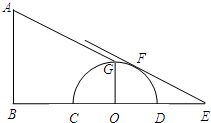 圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.
圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.
(1)求线段EF的长;
(2)求电线杆AB的高度.
 圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.
圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.(1)求线段EF的长;
(2)求电线杆AB的高度.
分析:(1)首先连接OF,由EF与⊙O相切,OF=3米,OE=5米,在Rt△OEF中,利用勾股定理即可求得线段EF的长;
(2)过点O作OH∥AG交AB于点H,即可得四边形AGOH是平行四边形,易证得△OBH∽△EFO,即可求得BH与AH的长,继而求得电线杆AB的高度.
(2)过点O作OH∥AG交AB于点H,即可得四边形AGOH是平行四边形,易证得△OBH∽△EFO,即可求得BH与AH的长,继而求得电线杆AB的高度.
解答: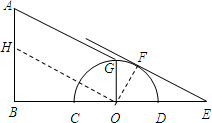 解:(1)连接OF,
解:(1)连接OF,
∵半圆的直径CD=6米,DE=2米,BC=5米,
∴OF=OD=OC=3米,OE=OD+DE=3+2=5(米),OB=BC+OC=5+3=8(米),
根据题意可得EF与⊙O相切,OF=3米,OE=5米,
∴OF⊥EF,
∴∠OFE=90°,
在Rt△OEF中,EF=
=4(米); …(4分)
(2)过点O作OH∥AG交AB于点H,
∵OH∥AG,
∴四边形AGOH是平行四边形,
∴AH=OG=3米,∠BOH=∠E,
∵∠B=∠OFE=90°,
∴△OBH∽△EFO,
∴
=
,
即
=
,
∴HB=6,
∴AB=HB+AH=6+3=9(米). …(10分)
 解:(1)连接OF,
解:(1)连接OF,∵半圆的直径CD=6米,DE=2米,BC=5米,
∴OF=OD=OC=3米,OE=OD+DE=3+2=5(米),OB=BC+OC=5+3=8(米),
根据题意可得EF与⊙O相切,OF=3米,OE=5米,
∴OF⊥EF,
∴∠OFE=90°,
在Rt△OEF中,EF=
| OE2-OF2 |
(2)过点O作OH∥AG交AB于点H,
∵OH∥AG,
∴四边形AGOH是平行四边形,
∴AH=OG=3米,∠BOH=∠E,
∵∠B=∠OFE=90°,
∴△OBH∽△EFO,
∴
| HB |
| OF |
| OB |
| EF |
即
| HB |
| 3 |
| 8 |
| 4 |
∴HB=6,
∴AB=HB+AH=6+3=9(米). …(10分)
点评:此题考查了切线的性质、相似三角形的判定与性质、平行四边形的性质以及勾股定理的应用.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
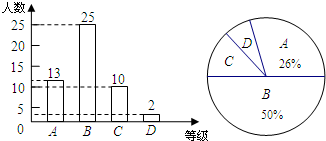 (2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:
(2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空: (2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为
(2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为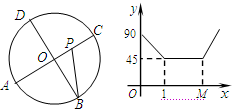 (2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为
(2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为