题目内容
对于抛物线y=（x-3）2+2与y=2（x-3）2+1，下列叙述错误的是（ ）A．开口方向相同
B．顶点坐标相同
C．对称轴相同
D．图象都在x轴上方
【答案】分析：根据二次函数的性质，结合两函数顶点式形式，即可得出两二次函数的顶点坐标以及对称轴和图象位置，分别分析即可．
解答：解：∵抛物线y=（x-3）2+2，
∴此函数顶点坐标为：（3，2），对称轴为：x=3，a=1＞0，开口向上，图象在x轴上方，
∵y=2（x-3）2+1，
∴此函数顶点坐标为：（3，1），对称轴为：x=3，a=2＞0，开口向上，图象在x轴上方，
∴A、开口方向相同，正确，不符合题意；
B、顶点坐标相同，错误，符合题意；
C、对称轴相同，正确，不符合题意；
D、图象都在x轴上方，正确，不符合题意．
故选：B．
点评：此题主要考查了二次函数的性质，根据顶点式得出二次函数性质是中考中考查重点，同学们应熟练掌握．
解答：解：∵抛物线y=（x-3）2+2，
∴此函数顶点坐标为：（3，2），对称轴为：x=3，a=1＞0，开口向上，图象在x轴上方，
∵y=2（x-3）2+1，
∴此函数顶点坐标为：（3，1），对称轴为：x=3，a=2＞0，开口向上，图象在x轴上方，
∴A、开口方向相同，正确，不符合题意；
B、顶点坐标相同，错误，符合题意；
C、对称轴相同，正确，不符合题意；
D、图象都在x轴上方，正确，不符合题意．
故选：B．
点评：此题主要考查了二次函数的性质，根据顶点式得出二次函数性质是中考中考查重点，同学们应熟练掌握．
练习册系列答案
相关题目
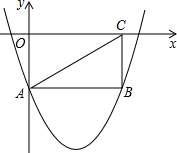如图，矩形OABC的两边在坐标轴上，且A（0，-2），AB=4，连接AC，抛物线y=x2+bx+c经过A，B两点．点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动．