题目内容
18、已知抛物线当x=2时有最小值-4,且抛物线过点A(3,0),则求该抛物线的解析式?
分析:由已知得抛物线顶点坐标为(2,-4),设顶点式,将A(3,0)代入顶点式求a即可.
解答:解:由题意:抛物线的顶点为(2,-4),
设抛物线解析式为y=a(x-2)2-4
把A(3,0)代入,得a-4=0,解得a=4,
∴抛物线解析式为y=4(x-2)2-4.
设抛物线解析式为y=a(x-2)2-4
把A(3,0)代入,得a-4=0,解得a=4,
∴抛物线解析式为y=4(x-2)2-4.
点评:本题考查了用待定系数法求二次函数解析式的方法.关键是根据条件确定抛物线解析式的形式,再求其中的待定系数.一般式:y=ax2+bx+c(a≠0);顶点式y=a(x-h)2+k,其中顶点坐标为(h,k);交点式y=a(x-x1)(x-x2),抛物线与x轴两交点为(x1,0),(x2,0).

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知抛物线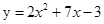 ,当自变量取两个不同的数值
,当自变量取两个不同的数值 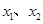 时,函数值相等,则当自变量
时,函数值相等,则当自变量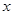 取
取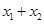 时的函数值与( )
时的函数值与( )
A.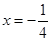 时,函数值相等 时,函数值相等 | B.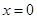 时,函数值相等 时,函数值相等 |
C.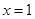 时,函数值相等 时,函数值相等 | D.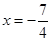 时,函数值相等 时,函数值相等 |
 已知抛物线y=-x2-2mx-m2+2m+1的顶点坐标为(-1,3),
已知抛物线y=-x2-2mx-m2+2m+1的顶点坐标为(-1,3),
 (2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0,
(2013•株洲)已知抛物线C1的顶点为P(1,0),且过点(0,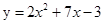 ,当自变量取两个不同的数值
,当自变量取两个不同的数值  时,函数值相等,则当自变量
时,函数值相等,则当自变量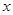 取
取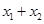 时的函数值与( )
时的函数值与( )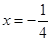 时,函数值相等 B.
时,函数值相等 B. 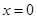 时,函数值相等
时,函数值相等
 时,函数值相等
D.
时,函数值相等
D. 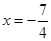 时,函数值相等
时,函数值相等