题目内容
工人师傅用一块矩形铁皮制作一个底面半径为10cm,高为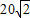 cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )
cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )A.(45,
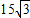 )
)B.(45,30)
C.(
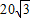 ,30)
,30)D.(
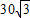 ,30)
,30)
【答案】分析:利用勾股定理可得圆锥的母线长,进而可求得圆锥的弧长,利用弧长公式可求得圆锥侧面展开图的圆心角的度数,可让圆锥侧面展开图的半径与矩形的长边重合,且与矩形长边相切,利用60°的三角函数求值即可.
解答: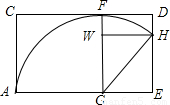 解:∵圆锥的底面半径为10cm,高为
解:∵圆锥的底面半径为10cm,高为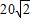 cm,
cm,
∴圆锥的母线长为30cm,底面周长为20πcm;
设圆锥的侧面展开图的圆心角的度数为n,则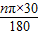 =20π,
=20π,
解得n=120°,
放在矩形中可得最省料的短边长为30cm,
长边长为30+30×cos60°=45cm,
故选B.
点评:用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;圆锥的底面半径,母线长,高组成直角三角形,可利用勾股定理求解;难点是得到圆锥侧面积相对于矩形的具体摆放位置.
解答:
 解:∵圆锥的底面半径为10cm,高为
解:∵圆锥的底面半径为10cm,高为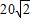 cm,
cm,∴圆锥的母线长为30cm,底面周长为20πcm;
设圆锥的侧面展开图的圆心角的度数为n,则
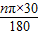 =20π,
=20π,解得n=120°,
放在矩形中可得最省料的短边长为30cm,
长边长为30+30×cos60°=45cm,
故选B.
点评:用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;圆锥的底面半径,母线长,高组成直角三角形,可利用勾股定理求解;难点是得到圆锥侧面积相对于矩形的具体摆放位置.

练习册系列答案
相关题目
工人师傅用一块矩形铁皮制作一个底面半径为10cm,高为20
cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )
| 2 |
A、(45,15
| ||
| B、(45,30) | ||
C、(20
| ||
D、(30
|
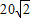 cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )
cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )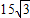 )
)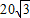 ,30)
,30)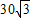 ,30)
,30)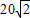 cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )
cm的圆锥形漏斗,(要求只能一次接缝,接缝处的材料不计)要最省料,你认为应选用下列规格(长,宽)中的( )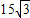 )
)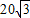 ,30)
,30)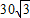 ,30)
,30)