Question

如图，在直角坐标系中，点A、B的坐标分别为（-3，0）、（0，3）．
（1）一次函数图象上的两点P、Q在直线AB的同侧，且直线PQ与y轴交点的纵坐标大于3，若△PAB与△QAB的面积都等于3，求这个一次函数的解析式；
（2）二次函数的图象经过点A、B，其顶点C在x轴的上方且在直线PQ上，求这个二次函数的解析式；
（3）若使（2）中所确定的抛物线的开口方向不变，顶点C在直线PQ上运动，当点C运动到点C′时，抛物线在x轴上截得的线段长为6，求点C′的坐标．

Answer 1

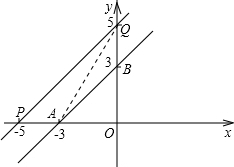解：（1）由已知，不妨设直线PQ与x轴、y轴的交点分别为P、Q；
∵S_△QAB=3，即BQ•AO=3，而AO=3，可求得BQ=2；
∵直线PQ与y轴交点的纵坐标大于3，
∴点Q的坐标为（0，5）；
同样可求得PA=2；
由于P、Q两点在直线AB的同侧，
所以点P的坐标为（-5，0）；
设直线PQ的解析式为y=kx+b，则
，
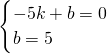解得，
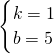因此所求一次函数的解析式为y=x+5；

（2）设二次函数的解析式为y=ax²+bx+c；
∵二次函数的图象过A（-3，0）、B（0，3）两点，
∴9a-3b+c=0 ①，c=3 ②
将②代入①，
解得b=3a+1；
于是二次函数的解析式为y=ax²+（3a+1）x+3；
其顶点C的坐标为（）；
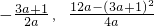∵点C在直线y=x+5上，
∴=；
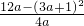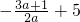整理，得9a²+8a-1=0，
解这个方程，得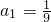，a₂=-1；
经检验a₁=，a₂=-1都是原方程的根；
但抛物线的顶点C在x轴的上方，且过A、B两点，
所以抛物线开口向下，将a=舍去，取a=-1；
∴所求的二次函数的解析式为y=-x²-2x+3；

（3）解法一：设点C′的横坐标为m；
由于点C′在直线y=x+5上，可求出点C′的纵坐标为m+5；
即点C′的坐标为（m，m+5）；
则运动后以C′为顶点的抛物线的解析式为
y=-（x-m）²+m+5；
设运动后的抛物线在对称轴右侧与x轴交点的横坐标为x₀，
由已知，有x₀=m+3；
即抛物线与x轴一个交点的坐标为（m+3，0）
∴0=-（m+3-m）²+m+5；
解得m=4；
∴m+5=9，于是点C′的坐标为（4，9）；
解法二：
同解法一求得以C′为顶点的抛物线的解析式为y=-（x-m）²+m+5；
即y=-x²+2mx-m²+m+5，
设这条抛物线与x轴的交点为（x₁，0）、（x₂，0）
∴x₁+x₂=2m，x₁•x₂=m²-m-5；
由已知|x₁-x₂|=6，
则（x₁-x₂）²=（x₁+x₂）²-4x₁x₂=36，即（2m）²-4（m²-m-5）=36，
解得m=4；
∴m+5=9，于是点C′的坐标为（4，9）．
分析：（1）由于PQ与y轴的交点纵坐标大于3，则P、Q同在直线AB的左侧；可设P在x轴上，Q在y轴上，根据△PAB与△QAB的面积即可求出PA、QB的长，由此可得到P、Q的坐标，即可求出直线PQ的解析式；
（2）设抛物线的解析式为y=ax²+bx+c，根据B点的坐标，可确定c的值，根据A点的坐标可求出a、b的关系式；进而可用a表示出抛物线的解析式，然后表示出顶点的坐标，由于顶点在直线PQ上，可将其代入直线PQ的解析式中，即可求出待定系数a的值，由此可得到抛物线的解析式；
（3）可设C′的横坐标为m，根据直线PQ的解析式即可确定其纵坐标，由此可得到平移后的函数解析式；进而可求出其与x轴交点的坐标，再根据两个交点间的距离为6，可列出关于m的方程，进而求出C′的坐标．
点评：此题主要考查了三角形面积的求法、二次函数解析式的确定、二次函数图象的平移、根与系数的关系等重要知识点，综合性强，难度较大．