题目内容
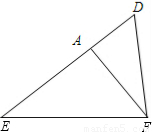
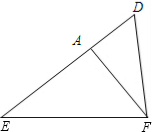如图，△DEF中，∠EDF=2∠E，FA⊥DE于点A，问：DF、AD、AE间有什么样的三边大小关系？
DF+AD=AE，
证明：在AE上取一点B，使AB=AD，
∵FA⊥DE，
∴FA垂直平分BD，
∴FD=FB，
∠FBD=∠D=2∠E，
∴∠FBD=2∠E，∠FBD是△BEF的外角，
∴∠FBD=∠E+∠BFE，
∴∠E=∠BFE，
∴BE=BF，
∴BE=DF，
∴AE=AB+BE=AD+DF．
分析：欲证三边之间的关系，即需要将三边联系起来，故在AE上去AB=AD，结合题意，可得∠FBD=∠D∠D=2∠E，再利用三角形的外角关系，可得出∠E=∠BFE，从而了得出AE=AB+BE=AD+DF．
点评：本题主要考查了垂线段在三角形的实际应用，属于中等题目，要求学生能够熟练掌握其性质．
证明：在AE上取一点B，使AB=AD，
∵FA⊥DE，
∴FA垂直平分BD，
∴FD=FB，
∠FBD=∠D=2∠E，
∴∠FBD=2∠E，∠FBD是△BEF的外角，
∴∠FBD=∠E+∠BFE，
∴∠E=∠BFE，
∴BE=BF，
∴BE=DF，
∴AE=AB+BE=AD+DF．
分析：欲证三边之间的关系，即需要将三边联系起来，故在AE上去AB=AD，结合题意，可得∠FBD=∠D∠D=2∠E，再利用三角形的外角关系，可得出∠E=∠BFE，从而了得出AE=AB+BE=AD+DF．
点评：本题主要考查了垂线段在三角形的实际应用，属于中等题目，要求学生能够熟练掌握其性质．
练习册系列答案
相关题目
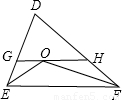
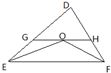15、如图，△DEF中，∠DEF、∠DFE的平分线相于点O，直线GH过点O与EF平行，分别与DE、DF交于点G、H．且DE=8，DF=7，则△DGH的周长=
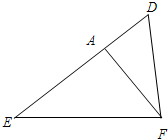23、如图，△DEF中，∠EDF=2∠E，FA⊥DE于点A，问：DF、AD、AE间有什么样的三边大小关系？
