题目内容
如图，点A的坐标为（2，2），点B的坐标为（3，0）．（1）请在直角坐标中画出△ABC绕着点C逆时针旋转90°后的图形△DEC，使D点对应A点，E点对应B点；
（2）写出点D、E的坐标；
（3）求线段DB长．
分析：（1）将三角形三个顶点A，B绕着点C逆时针旋转90°，找到旋转后的对应点然后再顺次连接；
（2）从图中可以读出点D，E的坐标；
（3）连接BD，会发现BD在网格中，正好是一个直角三角形的斜边，利用勾股定理就可求出．
（2）从图中可以读出点D，E的坐标；
（3）连接BD，会发现BD在网格中，正好是一个直角三角形的斜边，利用勾股定理就可求出．
解答：
解：（1）如图
（2）D（-3，1），E（-1，2）；
（3）在直角△DBM中，DM=1，BM=6，
∵DB2=DM2+MB2，
∴DB=
．
解：（1）如图（2）D（-3，1），E（-1，2）；
（3）在直角△DBM中，DM=1，BM=6，
∵DB2=DM2+MB2，
∴DB=
| 37 |
点评：本题考查旋转变换作图，做这类题的关键是找旋转后的对应点．但本题中也考查了勾股定理的应用．
练习册系列答案
相关题目
（2012•桂平市三模）如图，点P的坐标为（2，
已知：在直角坐标系中，点C的坐标为（0，-2），点A与点B在x轴上，且点A与点B的横坐标是方程x2-3x-4=0的两个根，点A在点B的左侧．
如图，点A的坐标为（-1，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为
如图，点A的坐标为（ ）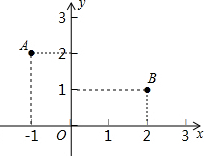
如图，点A的坐标为（-1，2），点B的坐标为（2，1），有一点C在x轴上移动，则点C到A、B两点的距离之和的最小值为（ ）