题目内容
(2012•汉沽区一模)在平面直角坐标系中,点A在坐标原点,B(6,0),C(6,8).折叠三角形ABC,使直角顶点B落在y轴上的T处.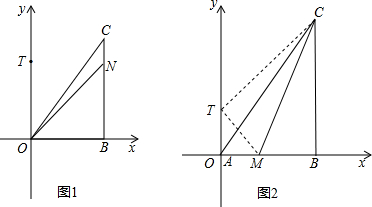
(1)如图1,折痕为AN,点N在BC上,求点T、点N的坐标;
(2)如图2,折痕为CM,点M在AB上,若设AT=x,
①用含x的代数式表示BM;
②求点M的坐标.

(1)如图1,折痕为AN,点N在BC上,求点T、点N的坐标;
(2)如图2,折痕为CM,点M在AB上,若设AT=x,
①用含x的代数式表示BM;
②求点M的坐标.
分析:(1)连接TN,TB,求出AB=6,BC=8,根据折叠的性质得出△ATN≌△ABT,推出∠OTN=∠ABC=90°=∠TAB,得出四边形TABN是矩形,推出∠TNB=90°,NT=AB=6,BN=OT=6,即可得出T的坐标、N的坐标;
(2)①根据沿CM折叠B和T重合得出BM=TM,在Rt△TOM中,由勾股定理得出OT2+AM2=TM2,代入求出即可;
②设AM=a,则BM=6-a,过C作CD⊥y轴于D,得出四边形DCBA是矩形,推出CD=AB=6,根据折叠的性质得出△TMC≌△BMC,推出BC=CT=8,∠CTM=∠MBC=90°,TM=BM=6-a,由勾股定理得DT=2
,证△CDT∽△TAM,推出
=
,代入求出即可.
(2)①根据沿CM折叠B和T重合得出BM=TM,在Rt△TOM中,由勾股定理得出OT2+AM2=TM2,代入求出即可;
②设AM=a,则BM=6-a,过C作CD⊥y轴于D,得出四边形DCBA是矩形,推出CD=AB=6,根据折叠的性质得出△TMC≌△BMC,推出BC=CT=8,∠CTM=∠MBC=90°,TM=BM=6-a,由勾股定理得DT=2
| 7 |
| DT |
| AM |
| CT |
| TM |
解答: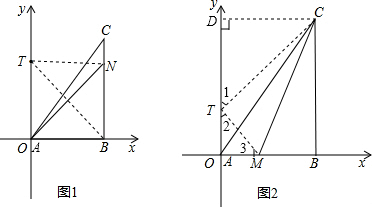
解:(1)连接TN,TB,
∵点A在坐标原点,B(6,0),C(6,8),
∴AB=6,BC=8,
∵∠ABC=∠TAB=90°,B沿AN折叠与T重合,
∴△ATN≌△ABT,
∴OT=AB=6,∠OTN=∠ABC=90°=∠TAB,
∴四边形TABN是矩形,
∴∠TNB=90°,NT=AB=6,BN=OT=6,
∴T的坐标是(0,6),N的坐标是(6,6);
(2)①∵沿CM折叠B和T重合,
∴BM=TM,
在Rt△TOM中,OT2+AM2=TM2,
即x2+(6-BM)2=BM2,
解得:BM=
x2+3;
②设AM=a,则BM=6-a,
过C作CD⊥y轴于D,
∵∠DAB=∠ABC=90°,
∴∠CDA=∠DAB=∠ABC=90°,
∴四边形DCBA是矩形,
∴CD=AB=6,
∵沿CM折叠B和T重合,
∴△TMC≌△BMC,
∴BC=CT=8,∠CTM=∠MBC=90°,TM=BM=6-a,
在Rt△CDT中,CD=6,CT=8,由勾股定理得:DT=2
,
∵∠DAB=90°,
∴∠2+∠3=90°,∠2+∠1=90°,
∴∠1=∠3,
∵∠CDT=∠TAM=90°,
∴△CDT∽△TAM,
∴
=
,
∴
=
,
a=
,
即M的坐标是(
,0).

解:(1)连接TN,TB,
∵点A在坐标原点,B(6,0),C(6,8),
∴AB=6,BC=8,
∵∠ABC=∠TAB=90°,B沿AN折叠与T重合,
∴△ATN≌△ABT,
∴OT=AB=6,∠OTN=∠ABC=90°=∠TAB,
∴四边形TABN是矩形,
∴∠TNB=90°,NT=AB=6,BN=OT=6,
∴T的坐标是(0,6),N的坐标是(6,6);
(2)①∵沿CM折叠B和T重合,
∴BM=TM,
在Rt△TOM中,OT2+AM2=TM2,
即x2+(6-BM)2=BM2,
解得:BM=
| 1 |
| 12 |
②设AM=a,则BM=6-a,
过C作CD⊥y轴于D,
∵∠DAB=∠ABC=90°,
∴∠CDA=∠DAB=∠ABC=90°,
∴四边形DCBA是矩形,
∴CD=AB=6,
∵沿CM折叠B和T重合,
∴△TMC≌△BMC,
∴BC=CT=8,∠CTM=∠MBC=90°,TM=BM=6-a,
在Rt△CDT中,CD=6,CT=8,由勾股定理得:DT=2
| 7 |
∵∠DAB=90°,
∴∠2+∠3=90°,∠2+∠1=90°,
∴∠1=∠3,
∵∠CDT=∠TAM=90°,
∴△CDT∽△TAM,
∴
| DT |
| AM |
| CT |
| TM |
∴
2
| ||
| a |
| 8 |
| 6-a |
a=
8
| ||
| 3 |
即M的坐标是(
8
| ||
| 3 |
点评:本题综合考查了相似的性质和判定,折叠的性质,勾股定理,一次函数的应用等知识点的运用,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
 (2012•汉沽区一模)如图,AB是⊙O的弦,⊙O的半径为5,OC⊥AB于D,交⊙O于点C,且CD=1,则弦AB的长为( )
(2012•汉沽区一模)如图,AB是⊙O的弦,⊙O的半径为5,OC⊥AB于D,交⊙O于点C,且CD=1,则弦AB的长为( ) (2012•汉沽区一模)△ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )
(2012•汉沽区一模)△ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )