题目内容
在“六•一”儿童节来临之际,某儿童商场用2800元购进了一批玩具,上市后很快脱销,商场又用7200元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了4元.
(1)该商场两次共购进这批玩具多少个?
(2)如果这两批玩具每个的售价相同,且全部售完后总利润率不低于20%,那么每个玩具售价至少是多少元?
解:(1)设该商场第一批购进了这种玩具x个,则第二批购进这种玩具2x个,由题意得:
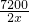 -
- =4,
=4,
解得:x=200,
经检验:x=200是原分式方程的解,
则2x=2×200=400,
200+400=600(个).
答:该商场两次共购进这批玩具600个;
(2)设每个玩具的售价为y元,根据题意得:
600y-(2800+7200)≥(2800+7200)×20%,
解得:y≥20,
则每个玩具的售价为20元.
答:每个玩具的售价至少为20元.
分析:(1)设该商场第一批购进了这种玩具x个,则第二批购进这种玩具2x个,根据关键语句“每个进价多了4元”可得方程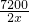 -
- =4,解方程即可;
=4,解方程即可;
(2)设每个玩具的售价为y元,根据题意可得不等关系:玩具的总售价-成本≥利润,由不等关系列出不等式即可.
点评:此题主要考查了分式方程,以及不等式的应用,关键是弄清题意,找出题目中的等量关系以及不等关系,列出方程与不等式.
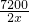 -
- =4,
=4,解得:x=200,
经检验:x=200是原分式方程的解,
则2x=2×200=400,
200+400=600(个).
答:该商场两次共购进这批玩具600个;
(2)设每个玩具的售价为y元,根据题意得:
600y-(2800+7200)≥(2800+7200)×20%,
解得:y≥20,
则每个玩具的售价为20元.
答:每个玩具的售价至少为20元.
分析:(1)设该商场第一批购进了这种玩具x个,则第二批购进这种玩具2x个,根据关键语句“每个进价多了4元”可得方程
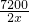 -
- =4,解方程即可;
=4,解方程即可;(2)设每个玩具的售价为y元,根据题意可得不等关系:玩具的总售价-成本≥利润,由不等关系列出不等式即可.
点评:此题主要考查了分式方程,以及不等式的应用,关键是弄清题意,找出题目中的等量关系以及不等关系,列出方程与不等式.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 转盘,那么可直接获得15元的购物券.
转盘,那么可直接获得15元的购物券.