题目内容
(2011•黑河)已知:二次函数y=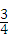 x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣
x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣ ).
).(1)求此二次函数的解析式.
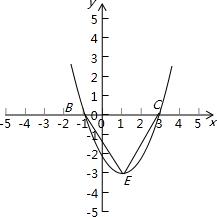
(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC的面积最大,并求出最大面积.
注:二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=﹣
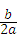 .
.
解:(1)由已知条件得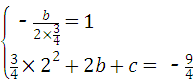 ,(2分)
,(2分)
解得b=﹣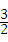 ,c=﹣
,c=﹣ ,
,
∴此二次函数的解析式为y=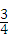 x2﹣
x2﹣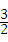 x﹣
x﹣ ;(1分)
;(1分)
(2)∵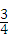 x2﹣
x2﹣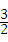 x﹣
x﹣ =0,
=0,
∴x1=﹣1,x2=3,
∴B(﹣1,0),C(3,0),
∴BC=4,(1分)
∵E点在x轴下方,且△EBC面积最大,
∴E点是抛物线的顶点,其坐标为(1,﹣3),(1分)
∴△EBC的面积=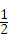 ×4×3=6.(1分)解析:
×4×3=6.(1分)解析:
略
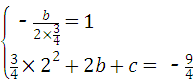 ,(2分)
,(2分)解得b=﹣
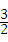 ,c=﹣
,c=﹣ ,
,
∴此二次函数的解析式为y=
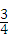 x2﹣
x2﹣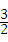 x﹣
x﹣ ;(1分)
;(1分)(2)∵
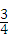 x2﹣
x2﹣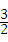 x﹣
x﹣ =0,
=0,∴x1=﹣1,x2=3,
∴B(﹣1,0),C(3,0),
∴BC=4,(1分)
∵E点在x轴下方,且△EBC面积最大,
∴E点是抛物线的顶点,其坐标为(1,﹣3),(1分)
∴△EBC的面积=
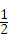 ×4×3=6.(1分)解析:
×4×3=6.(1分)解析:略

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
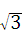 x+4
x+4
 x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣
x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣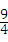 ).
).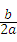 .
.