题目内容
在直角坐标系中，抛物线y=x2-2mx+n+1的顶点为A，与y轴交于点B，抛物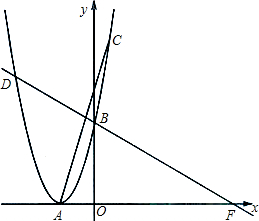
线上的一点C的横坐标为1，且AC=3| 10 |
（1）用配方法把解析式y=x2-2mx+n+1化成y=a（x-h）2+k的形式；用含m、n的代数式表示顶点A的坐标；
（2）如果顶点A在x轴负半轴上，求此抛物线的函数关系式；
（3）在（2）中的抛物线上有一点D，使得直线DB经过第一、二、四象限，
交x轴于点F，且原点O到直线DB的距离为
| 8 |
| 5 |
| 5 |
分析：（1）把抛物线利用配方法变为顶点形式，即可找出顶点A的坐标；
（2）过C作CE垂直于x轴，由点C的横坐标为1，把x=1代入抛物线解析式表示出C的纵坐标，且纵坐标大于0，即为CE的长，同时得到OE等于C的横坐标，由抛物线A在x轴负半轴上，得到A的横坐标小于0，纵坐标等于0，表示出A的坐标，同时根据纵坐标为0列出m与n的关系式，记作①，根据OA与OE的和表示出AE，且由AC及CE的长，在直角三角形ACE中，利用勾股定理列出m与n的另一个关系式，记作②，把①代入②消去n得到关于m的方程，求出方程的解得到m的值，把m的值代入①求出n的值，即可确定出抛物线的解析式；
（3）由直线DB过第一、二、四象限设直线DB与x轴正半轴交于F，过O作OM垂直于直线DB，由已知O到直线DB的距离得到OM的长，根据（2）求出的抛物线解析式，令x=0求出y的值，确定出B的坐标，即可得到OB的长，在直角三角形OBM中，由OB及OM的长，利用勾股定理求出BM的长，由OB⊥OF，OM⊥BF，根据同角的余角相等得到一对锐角相等，再由一对直角相等，利用两对对应角相等的两三角形相似得到三角形BOM与三角形MOF相似，根据相似得比例，由MB和OM的长即可得到OF=2OB，即可求出OF的长，得到F的坐标，设出直线BF的解析式为y=kx+b，把B和F坐标代入确定出k与b的值，从而得到直线FB的方程，把抛物线解析式与直线FB联立，即可求出交点D的坐标．
（2）过C作CE垂直于x轴，由点C的横坐标为1，把x=1代入抛物线解析式表示出C的纵坐标，且纵坐标大于0，即为CE的长，同时得到OE等于C的横坐标，由抛物线A在x轴负半轴上，得到A的横坐标小于0，纵坐标等于0，表示出A的坐标，同时根据纵坐标为0列出m与n的关系式，记作①，根据OA与OE的和表示出AE，且由AC及CE的长，在直角三角形ACE中，利用勾股定理列出m与n的另一个关系式，记作②，把①代入②消去n得到关于m的方程，求出方程的解得到m的值，把m的值代入①求出n的值，即可确定出抛物线的解析式；
（3）由直线DB过第一、二、四象限设直线DB与x轴正半轴交于F，过O作OM垂直于直线DB，由已知O到直线DB的距离得到OM的长，根据（2）求出的抛物线解析式，令x=0求出y的值，确定出B的坐标，即可得到OB的长，在直角三角形OBM中，由OB及OM的长，利用勾股定理求出BM的长，由OB⊥OF，OM⊥BF，根据同角的余角相等得到一对锐角相等，再由一对直角相等，利用两对对应角相等的两三角形相似得到三角形BOM与三角形MOF相似，根据相似得比例，由MB和OM的长即可得到OF=2OB，即可求出OF的长，得到F的坐标，设出直线BF的解析式为y=kx+b，把B和F坐标代入确定出k与b的值，从而得到直线FB的方程，把抛物线解析式与直线FB联立，即可求出交点D的坐标．
解答：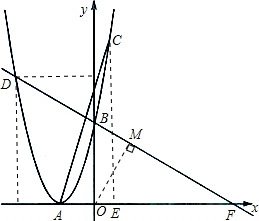
解：（1）配方得：y=（x-m）2+（-m2+n+1），
所以顶点A（m，-m2+n+1）；
（2）根据题意，如图所示，过点C作CE⊥x轴交于点E，
∵抛物线上一点C的横左边为1，且AC=3
，
∴C（1，n-2m+2），其中n-2m+2＞0，OE=1，CE=n-2m+2，
∵抛物线的顶点在x轴的负半轴上，
∴A（m，0），n=m2-1①，
其中m＜0，OA=-m，则AE=OE+OA=1-m，
在Rt△ACE中，根据勾股定理得：AE2+CE2=AC2，
即（1-m）2+（n-2m+2）2=（3
）2②，
把①代入②得：（m2-2m+1）2+（m2-2m+1）-90=0，
∴（m2-2m+11）（m2-2m-8）=0，
∴m2-2m+11=0或m2-2m-8=0，
方程m2-2m+11=0，∵△=b2-4ac=4-44=-40＜0，∴方程无解；
方程m2-2m-8=0，分解因式得：（m-4）（m+2）=0，解得：m1=4，m2=-2，
∵m＜0，∴m=-2，
把m=-2代入①得：n=4-1=3，
∴抛物线解析式为y=x2+4x+4；
（3）∵直线DB经过第一、二、四象限，
设直线DB交x轴正半轴于点F，过点O作OM⊥DB于点M，
∵点O到直线DB的距离为
，∴OM=
，
∵抛物线y=x2+4x+4与y轴交于点B，∴B（0，4），∴OB=4，
在Rt△OBM中，根据勾股定理得：BM=
=
=
，
∵OB⊥OF，OM⊥BF，
∴∠OBM+∠BOM=90°，∠OBM+∠BFO=90°，
∴∠BOM=∠BFO，又∠OMB=∠OMF=90°，
∴△OBM∽△FOM，
∴
=
，即
=
，
∴OF=2BO=8，∴F（8，0），
设直线FB的方程为y=kx+b，
把F和B的坐标代入得：
，解得
，
∴直线BF解析式为y=-
x+4，
∵点D既在抛物线上，又在直线BF上，
∴
，解得：
或
，
∵BD为直线，∴点D与点B不重合，
∴点D的坐标为（-
，
）．
解：（1）配方得：y=（x-m）2+（-m2+n+1），所以顶点A（m，-m2+n+1）；
（2）根据题意，如图所示，过点C作CE⊥x轴交于点E，
∵抛物线上一点C的横左边为1，且AC=3
| 10 |
∴C（1，n-2m+2），其中n-2m+2＞0，OE=1，CE=n-2m+2，
∵抛物线的顶点在x轴的负半轴上，
∴A（m，0），n=m2-1①，
其中m＜0，OA=-m，则AE=OE+OA=1-m，
在Rt△ACE中，根据勾股定理得：AE2+CE2=AC2，
即（1-m）2+（n-2m+2）2=（3
| 10 |
把①代入②得：（m2-2m+1）2+（m2-2m+1）-90=0，
∴（m2-2m+11）（m2-2m-8）=0，
∴m2-2m+11=0或m2-2m-8=0，
方程m2-2m+11=0，∵△=b2-4ac=4-44=-40＜0，∴方程无解；
方程m2-2m-8=0，分解因式得：（m-4）（m+2）=0，解得：m1=4，m2=-2，
∵m＜0，∴m=-2，
把m=-2代入①得：n=4-1=3，
∴抛物线解析式为y=x2+4x+4；
（3）∵直线DB经过第一、二、四象限，
设直线DB交x轴正半轴于点F，过点O作OM⊥DB于点M，
∵点O到直线DB的距离为
8
| ||
| 5 |
8
| ||
| 5 |
∵抛物线y=x2+4x+4与y轴交于点B，∴B（0，4），∴OB=4，
在Rt△OBM中，根据勾股定理得：BM=
| OB2-OM2 |
42-(
|
4
| ||
| 5 |
∵OB⊥OF，OM⊥BF，
∴∠OBM+∠BOM=90°，∠OBM+∠BFO=90°，
∴∠BOM=∠BFO，又∠OMB=∠OMF=90°，
∴△OBM∽△FOM，
∴
| OB |
| MB |
| FO |
| MO |
| OB | ||||
|
| FO | ||||
|
∴OF=2BO=8，∴F（8，0），
设直线FB的方程为y=kx+b，
把F和B的坐标代入得：
|
|
∴直线BF解析式为y=-
| 1 |
| 2 |
∵点D既在抛物线上，又在直线BF上，
∴
|
|
|
∵BD为直线，∴点D与点B不重合，
∴点D的坐标为（-
| 9 |
| 2 |
| 25 |
| 4 |
点评：此题是一道二次函数的综合题，涉及的知识有相似三角形的判定与性质，勾股定理，直线与抛物线的交点坐标，一元二次方程的解法，一次函数的性质等，要求学生全面掌握所学知识，把所学知识融会贯通，利用数形结合的思想解决问题，作为压轴题，能有效地考查学生的理解能力，分析能力，对数学知识和数学方法的驾驭能力．
练习册系列答案
口算题天天练系列答案
相关题目
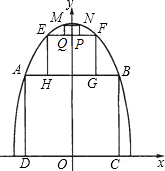为了参加市科技节展览，同学们制造了一个截面为抛物线形的隧道模型，用了三种正方形的钢筋支架．在画设计图时，如果在直角坐标系中，抛物线的函数解析式为y=-x2+c，正方形ABCD的边长和正方形EFGH的边长之比为5：1，求：
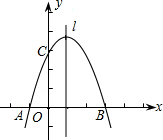，B，C三点的抛物的对称轴为直线l，D为对称轴l上一动点．
为了参加市科技节展览，同学们制造了一个截面为抛物线形的隧道模型，用了三种正方形的钢筋支架．在画设计图时，如果在直角坐标系中，抛物线的函数解析式为y=-x2+c，正方形ABCD的边长和正方形EFGH的边长之比为5：1，求：
（2005•杭州）为了参加市科技节展览，同学们制造了一个截面为抛物线形的隧道模型，用了三种正方形的钢筋支架．在画设计图时，如果在直角坐标系中，抛物线的函数解析式为y=-x2+c，正方形ABCD的边长和正方形EFGH的边长之比为5：1，求：