题目内容
当x同时满足3x-（2a-3）=4x+3a+6 和不等式
≤
+1时，求a的取值范围．
| 2x-1 |
| 3 |
| 5x+1 |
| 2 |
分析：先解方程3x-（2a-3）=4x+3a+6，求得x=-5a-3，再解不等式
≤
+1，得出x≥-1，由于x同时满足3x-（2a-3）=4x+3a+6 和不等式
≤
+1，所以-5a-3≥-1，解此不等式即可求出a的取值范围．
| 2x-1 |
| 3 |
| 5x+1 |
| 2 |
| 2x-1 |
| 3 |
| 5x+1 |
| 2 |
解答：解：解方程3x-（2a-3）=4x+3a+6，得x=-5a-3，
解不等式
≤
+1，得x≥-1，
由题意，得-5a-3≥-1，
解得a≤-
．
解不等式
| 2x-1 |
| 3 |
| 5x+1 |
| 2 |
由题意，得-5a-3≥-1，
解得a≤-
| 2 |
| 5 |
点评：本题考查了一元一次方程与一元一次不等式的解法，属于基础题，正确地求出方程的解与不等式的解集是解题的关键．
练习册系列答案
相关题目
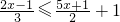时，求a的取值范围．
，
）]．
，
）]．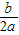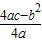