题目内容
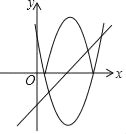
【题目】课堂上,老师给出一道题:如图,将抛物线C:y=x2﹣6x+5在x轴下方的图象沿x轴翻折,翻折后得到的图象与抛物线C在x轴上方的图象记为G,已知直线l:y=x+m与图象G有两个公共点,求m的取值范围甲同学的结果是﹣5<m<﹣1,乙同学的结果是m>![]() .下列说法正确的是( )
.下列说法正确的是( )
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
【答案】D
【解析】
当直线过抛物线与x轴右侧的交点时,恰有一个交点;
直线y=x+m向上移,经过g左侧交点之前均为两个交点;
继续向上平移,直到经过G中间的顶点(3,4)之前均为三个交点;
最终向上平移,均有两个交点.
解:令y=x2﹣6x+5=0,解得(1,0),(5,0)
将点(1,0),(5,0)分别代入直线y=x+m,得m=﹣1,﹣5;
∴﹣5<m<﹣1
由题可知,图象G中的顶点为(3,4)
代入直线y=x+m,得m=1,
∴m>1
综上所述,m>1或﹣5<m<﹣1
故选:D.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
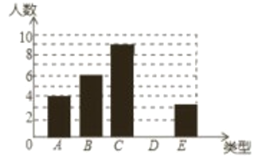
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
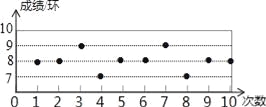
根据以上图表信息,参赛选手应选( )
A. 甲 B. 乙 C. 丙 D. 丁