题目内容
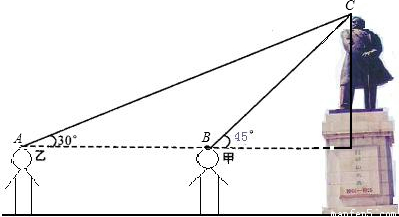
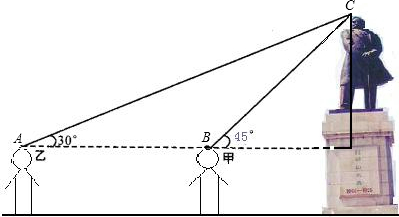
甲、乙两位学生为了将解直角三角形的知识学以致用，他们相约到孙文公园测量孙中山塑像及其底座的高度．下面是两位同学的一段对话：甲：我站在此处看塔顶仰角为45°，乙：我站在此处看塔顶仰角为30°．
甲：我们的身高都是1.6m，乙：我们相距4m．
请你根据两位同学的对话，计算孙中山塑像及其底座的高度大致是多少？（精确到0.1米，
| 3 |
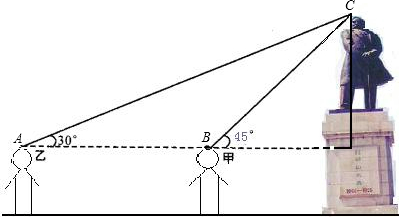
分析：根据三角形外角和定理，可求得∠CAB=30°，AB=4m．在Rt△CBD中，根据45°角的正弦值可求出CD，再加上同学自身的身高1.6m即可解答．
解答：解：如图所示，设甲、乙、头像顶部分别为B、A、C，作CD⊥AB的延长线于点D．…（1分）
设CD=xm，…（2分）
在Rt△ABC中，∠CBD=45°，所以BD=x，…（3分）
在Rt△ABC中，∠CAD=30°，所以AD=
x，…（4分）
由AB=AD-BD，且AB=4，可得
x-x=4…（5分）
解得，x=2（
+1）≈5.5…（6分）
由于5.5+1.6=7.1
所以头像的高度约为7.1m…（7分）
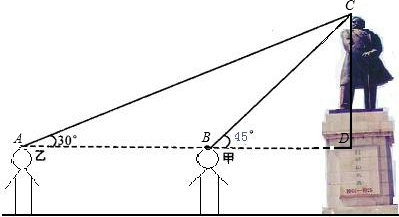
设CD=xm，…（2分）
在Rt△ABC中，∠CBD=45°，所以BD=x，…（3分）
在Rt△ABC中，∠CAD=30°，所以AD=
| 3 |
由AB=AD-BD，且AB=4，可得
| 3 |
解得，x=2（
| 3 |
由于5.5+1.6=7.1
所以头像的高度约为7.1m…（7分）
点评：此题考查的知识点是解直角三角形的应用-仰角俯角问题，关键本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
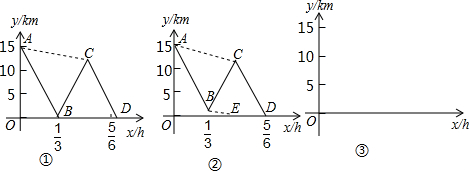
h．图②中折线A-B-C-D、线段AC、线段BE分别表示王老师、甲、乙在上述过程中，离车站的路程y（km）与王老师所用时间x（h）之间的函数关系．求a的值．
）．
）．