题目内容
【题目】如图,已知矩形ABCD中,AB=1,E是BC上一点,将△DCE沿DE翻折得到△DC′E.

(1) 如图1,若点B恰好在DC′的延长线上,且C′B=C′D,求CE的长;
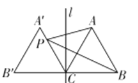
(2) 如图2,若点A恰好在EC′的延长线上,且C′A=2C′E,求BE的长.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)由折叠得到C′D=CD=1,得到BD=2,进而得到BC=![]() ,设CE=C′E=x,则BE=
,设CE=C′E=x,则BE=![]() -x,然后在Rt△BC′E中使用勾股定理即可求解.
-x,然后在Rt△BC′E中使用勾股定理即可求解.
(2)连接DE,由折叠得∠DEC=∠DEA,又∠DEC=∠ADE,得到∠DEA=∠ADE,得到△ADE为等腰三角形,设CE= C′E=y,则AE=AD=BC=3y,得到BE=2y,在Rt△ABE中使用勾股定理即可求解.
解:(1)∵四边形ABCD是矩形,∴CD=AB=1,∠C=90°
∵△DCE沿DE翻折得到△DC′E,∴CE=C′E,C′D=CD,∠EC′D=∠C=90°
∵C′B=C′D=C′D=CD=AB=1
∴BD=2,
在Rt△BCD中,由勾股定理可知BC=![]()
设CE=C′E=x,则BE=![]() -x
-x
在Rt△BC′E中,由勾股定理有:![]()
代入数据:![]()
解得:![]() ,即CE=
,即CE=![]()
故答案为:![]() .
.
(2)连接DE,如下图所示:

由折叠得∠DEC=∠DEA,
又∵AD∥BC,∴∠ADE=∠DEC
∴∠DEA=∠ADE
∴△ADE为等腰三角形
∴AE=AD
设CE= C′E=y,则AC′=2C′E =2y
∴BC=AD=AE= AC′+ C′E =2y+y=3y,
∴BE=BC-CE=3y-y=2y
在Rt△ABE中,由勾股定理得:![]()
代入数据得:![]()
解得:![]() ,即BE =2y=
,即BE =2y=![]()
故答案为:![]() .
.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目