题目内容
□ABCD中,AB⊥AC,AB=1,BC= ,对角线BD、AC交于点O. 将直线AC绕点O顺时针旋转分别交BC、AD于点E、F. (∠AOF为旋转角)
,对角线BD、AC交于点O. 将直线AC绕点O顺时针旋转分别交BC、AD于点E、F. (∠AOF为旋转角)
(1)试说明在旋转过程中,AF与CE总保持相等;
(2)证明:当∠AOF=90°时,四边形ABEF是平行四边形;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度. 
(1)∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,
∴∠FAO=∠ECO,
∴在△AOF和△COE中,
∠AOF=∠COE(对顶角相等)
∠FAO=∠EOC
AO=CO,
∴△AOF≌△COE,
∴CE=AF;
(2)AC旋转后的位置如图所示.
∵∠AOF=∠BAC=90°,
∴AB∥FE,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形ABEF是平行四边形;
(3)①可能.当EF⊥BD时,四边形BEDF是菱形.
∵△AOF≌△COE(已证)
∴EO=FO,
又∵四边形ABCD是平行四边形,
∴BO=DO,
又∵EF⊥BD,
∴四边形BEDF是菱形;
②∵AB=1,BC=
∴AC= =2,
=2,
∴AO=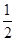 AC=1,
AC=1,
∴△ABO是等腰直角三角形,∠AOB=45°,
又∵∠BOF=90°,
∴∠AOF=45°,即旋转角为45°.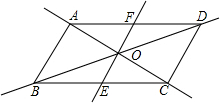
解析

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
如图,在?ABCD中,AB:AD=3:2,∠ADB=60°,那么cosA的值等于( )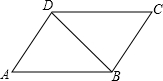

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 7、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,若AC=4则.①△CDE的周长比△CDA的周长小4,②∠ACD=90°;③AE=ED=CE;④四边形ABCD面积是12.则上述结论正确的是( )
7、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,若AC=4则.①△CDE的周长比△CDA的周长小4,②∠ACD=90°;③AE=ED=CE;④四边形ABCD面积是12.则上述结论正确的是( ) 14、如图,在矩形ABCD中,AB=6cm,将矩形ABCD折叠,使点B与点D重合,点C落在C′处,若AE:BE=1:2,则折痕EF的长为
14、如图,在矩形ABCD中,AB=6cm,将矩形ABCD折叠,使点B与点D重合,点C落在C′处,若AE:BE=1:2,则折痕EF的长为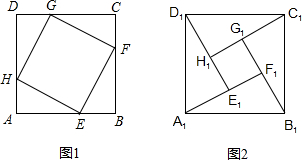
 5、如图,在等腰梯形ABCD中,AB∥DC,AB=998,DC=1001,AD=1999,点P在线段AD上,则满足条件∠BPC=90°的点P的个数为( )
5、如图,在等腰梯形ABCD中,AB∥DC,AB=998,DC=1001,AD=1999,点P在线段AD上,则满足条件∠BPC=90°的点P的个数为( )