题目内容
【题目】二次函数y=ax2+bx+c的图象如图所示,则下列式子中①abc<0;②0<b<-2a;③![]() ; ④a+b+c<0成立的个数有( )
; ④a+b+c<0成立的个数有( )
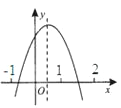
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
①∵图象开口向下,∴a<0,
∵图象与y轴交于正半轴,∴c>0,
∵对称轴在y轴右侧,故x=-![]() >0,b>0,
>0,b>0,
于是得abc<0,正确;
②由图对称轴:x=-![]() <1,可得b<-2a.
<1,可得b<-2a.
又b>0,∴0<b<-2a正确;
③∵0<-![]() <1,
<1,
∴2a+b<0,
∵c>0,
∴2a+b<c,
∴a<![]() ;正确
;正确
④当x=1时,a+b+c>0.此项错误
故选C.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目