题目内容
函数y=mx和函数y=x2-mx+m(m为常数)在同一个平面直角坐标系中的图象可以是( )
A. | B.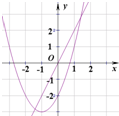 | C.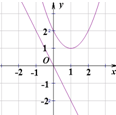 | D.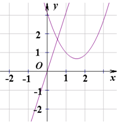 |
当m>0时,y=mx的图象是经过原点和一三象限的直线,
y=x2-mx+m开口向上,与y轴交于正半轴,对称轴是x=
>0,这时二次函数图象的对称轴在y轴右侧,
当mx=x2-mx+m时,x2-2mx+m=0,
△=4m2-4m=4(m2-m)=4(m-
)2-1,
∵m>0,
∴△=4(m-
)2-1>0,
∴有两个不同的实数根,
故函数y=mx和函数y=x2-mx+m(m为常数)在同一个平面直角坐标系中的图象有两个不同的交点,
故选:A.
y=x2-mx+m开口向上,与y轴交于正半轴,对称轴是x=
| m |
| 2 |
当mx=x2-mx+m时,x2-2mx+m=0,
△=4m2-4m=4(m2-m)=4(m-
| 1 |
| 2 |
∵m>0,
∴△=4(m-
| 1 |
| 2 |
∴有两个不同的实数根,
故函数y=mx和函数y=x2-mx+m(m为常数)在同一个平面直角坐标系中的图象有两个不同的交点,
故选:A.

练习册系列答案
相关题目

 的顶点坐标是 ,x 时,y随x的增大而增大.
的顶点坐标是 ,x 时,y随x的增大而增大.




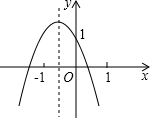

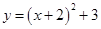 的顶点坐标是 【 】
的顶点坐标是 【 】