题目内容
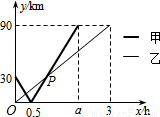
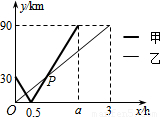
(2010•咸宁)在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.(1)填空:A、C两港口间的距离为______km,a=______;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)若两船的距离不超过10km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
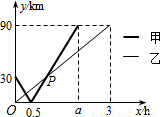
【答案】分析:(1)由甲船行驶的函数图象可以看出,甲船从A港出发,0.5h后到达B港,ah后到达C港,又由于甲船行驶速度不变,则可以求出a的值;
(2)分别求出0.5h后甲乙两船行驶的函数表达式,联立即可求解;
(3)将该过程划分为0≤x≤0.5、0.5<x≤1、1<x三个范围进行讨论,得到能够相望时x的取值范围.
解答:解:(1)A、C两港口间距离s=30+90=120km,
又由于甲船行驶速度不变,
故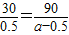 ,
,
则a=2(h).
(2)由点(3,90)求得,y2=30x.
当x>0.5时,由点(0.5,0),(2,90)求得,y1=60x-30.
当y1=y2时,60x-30=30x,
解得,x=1.
此时y1=y2=30.
所以点P的坐标为(1,30).
该点坐标的意义为:两船出发1h后,甲船追上乙船,此时两船离B港的距离为30km.
(3)①当x≤0.5时,由点(0,30),(0.5,0)求得,y1=-60x+30
依题意,(-60x+30)+30x≤10.解得,x≥ .不合题意.
.不合题意.
②当0.5<x≤1时,依题意,30x-(60x-30)≤10
解得,x≥ .所以
.所以 ≤x≤1.(8分)
≤x≤1.(8分)
③当x>1时,依题意,(60x-30)-30x≤10
解得,x≤ .所以1<x≤
.所以1<x≤ (9分)
(9分)
④当2≤x≤3时,甲船已经到了而乙船正在行驶,
∵90-30x≤10,解得x≥ ,
,
所以,当 ≤x≤3,甲、乙两船可以相互望见;
≤x≤3,甲、乙两船可以相互望见;
综上所述,当 ≤x≤
≤x≤ 时或当
时或当 ≤x≤3时,甲、乙两船可以相互望见.
≤x≤3时,甲、乙两船可以相互望见.
点评:此题为函数方程、函数图象与实际结合的问题,同学们应加强这方面的训练.
(2)分别求出0.5h后甲乙两船行驶的函数表达式,联立即可求解;
(3)将该过程划分为0≤x≤0.5、0.5<x≤1、1<x三个范围进行讨论,得到能够相望时x的取值范围.
解答:解:(1)A、C两港口间距离s=30+90=120km,
又由于甲船行驶速度不变,
故
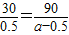 ,
,则a=2(h).
(2)由点(3,90)求得,y2=30x.
当x>0.5时,由点(0.5,0),(2,90)求得,y1=60x-30.
当y1=y2时,60x-30=30x,
解得,x=1.
此时y1=y2=30.
所以点P的坐标为(1,30).
该点坐标的意义为:两船出发1h后,甲船追上乙船,此时两船离B港的距离为30km.
(3)①当x≤0.5时,由点(0,30),(0.5,0)求得,y1=-60x+30
依题意,(-60x+30)+30x≤10.解得,x≥
 .不合题意.
.不合题意.②当0.5<x≤1时,依题意,30x-(60x-30)≤10
解得,x≥
 .所以
.所以 ≤x≤1.(8分)
≤x≤1.(8分)③当x>1时,依题意,(60x-30)-30x≤10
解得,x≤
 .所以1<x≤
.所以1<x≤ (9分)
(9分)④当2≤x≤3时,甲船已经到了而乙船正在行驶,
∵90-30x≤10,解得x≥
 ,
,所以,当
 ≤x≤3,甲、乙两船可以相互望见;
≤x≤3,甲、乙两船可以相互望见;综上所述,当
 ≤x≤
≤x≤ 时或当
时或当 ≤x≤3时,甲、乙两船可以相互望见.
≤x≤3时,甲、乙两船可以相互望见.点评:此题为函数方程、函数图象与实际结合的问题,同学们应加强这方面的训练.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目