题目内容
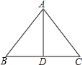
【题目】已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
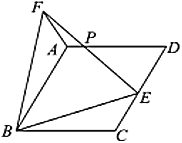
(2)如图c,在AB和AC上分别截取点B′和C′,使AB=![]() AB′,AC=
AB′,AC=![]() AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.

【答案】(1)①是,∠BOE=120°②∠BOE=120°(2)当0°<![]() <30°时,∠BOE=60°
<30°时,∠BOE=60°
当30°<![]() <180°时,∠BOE=120°
<180°时,∠BOE=120°
【解析】
试题(1)是∠BOE=120°
(2)由已知得:△ABC和△ADE是全等的等边三角形
∴AB=AD=AC=AE
∵△ADE是由△ABC绕点A旋转![]() 得到的
得到的
∴∠BAD=∠CAE=![]()
∴△BAD≌△CAE
∴∠ADB=∠AEC
∵∠ADB+∠ABD+∠BAD=180°
∴∠AEC+∠ABO+∠BAD=180°
∵∠ABO+∠AEC+∠BAE+∠BOE=360°
∵∠BAE=∠BAD+∠DAE
∴∠DAE+∠BOE=180°
又∵∠DAE=60°
∴∠BOE=120°
(3)如图
 ,
,
c在AB和AC上分别截取点B′和C′,使AB=![]() AB′,AC=
AB′,AC=![]() AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<![]() <180°),得到△ADE,AB=
<180°),得到△ADE,AB=![]() AB′,AC=
AB′,AC=![]() AC′,可得
AC′,可得![]() ,根据旋转的特征,所以
,根据旋转的特征,所以
当0°<![]() <30°时,∠BOE=60°
<30°时,∠BOE=60°
当30°<![]() <180°时,∠BOE=120°
<180°时,∠BOE=120°

【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题
(1)当x=3时,y=
(2)当x为何值时,y=0?
(3)①若自变量x的取值范围是0≤x≤5,求函数值y的取值范围;
②若函数值y为正数,则自变量x的取值范围.